

Next: Variance ratio smoothing
Up: Alternatives to the Random
Previous: Alternatives to the Random
Facing this dilemma of an invalid population analysis (fixed-effect approach) and a valid one
(random-effect) but difficult to apply usually because of overestimation of variances due to
small samples (random-effects), some alternatives have been investigated. One is the ``conjunction
analysis'' (Friston et al. [5]), which uses all the subjects' maps to localise
where all the subjects activated (at a chosen level; see single subject analysis, 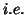 it is a
thresholded map of the
it is a
thresholded map of the  map over the subjects). Then using simple probability theory, one can
relate the ``level of activation'' (p-value calculated for example from Gaussian Random Field
Theory - see Worsley(1999 submitted)) and the proportion of the population which shows this
activation at the previously defined level (in the single-subject analysis). Let
map over the subjects). Then using simple probability theory, one can
relate the ``level of activation'' (p-value calculated for example from Gaussian Random Field
Theory - see Worsley(1999 submitted)) and the proportion of the population which shows this
activation at the previously defined level (in the single-subject analysis). Let 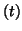 and
and 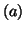 mean respectively, tested status of activation with the experiment and true status of
activation, while
mean respectively, tested status of activation with the experiment and true status of
activation, while 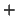 and
and  is the status activated or not, simple probability calculus
gives:
is the status activated or not, simple probability calculus
gives:
Where 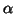 is the chosen single-subject level of activation (p-value level to threshold each
map),
is the chosen single-subject level of activation (p-value level to threshold each
map), 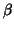 is the power or sensitivity (
is the power or sensitivity (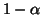 is the specificity) of the experiment which
is not known and can be set at
is the specificity) of the experiment which
is not known and can be set at 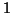 to provide a lower bound of the proportion
to provide a lower bound of the proportion 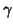 of the
population showing the effect. Setting
of the
population showing the effect. Setting 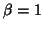 gives
gives
Thus the conclusion about the population is
qualitative, 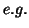 with a certainty of 0.95 (
with a certainty of 0.95 (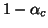 ), we can say that at least 80%
(
), we can say that at least 80%
(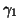 ) of the population would activate at level 0.001 (
) of the population would activate at level 0.001 (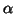 ). The results given above
can also be used to decide on a sample size[6],
). The results given above
can also be used to decide on a sample size[6],  for the above conclusion one
would need at least
for the above conclusion one
would need at least 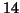 subjects.
Remarks:
The
subjects.
Remarks:
The 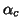 could be calculated using permutation testing procedure instead of using random
field theory. The conjunction could also be defined as a given proportion of subjects; this could
cope better with problems such as poor localisation due to registration problems, as conjunction
analysis is certainly very sensitive to subject outliers in terms of the locations of the
activations. If one decides that
could be calculated using permutation testing procedure instead of using random
field theory. The conjunction could also be defined as a given proportion of subjects; this could
cope better with problems such as poor localisation due to registration problems, as conjunction
analysis is certainly very sensitive to subject outliers in terms of the locations of the
activations. If one decides that  must activate to define a conjunction then given
must activate to define a conjunction then given 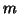 :
:
with
![$P(t_+)=[\alpha(1-\gamma)+\beta\gamma]$](img95.gif) as given above. One must notice that the amount of
conjunction
as given above. One must notice that the amount of
conjunction 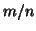 must be at least the expected
must be at least the expected 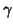 , otherwise the multiplicative function
introduced in the above equation is not monotonic with
, otherwise the multiplicative function
introduced in the above equation is not monotonic with 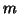 . This problem is also linked with
values of
. This problem is also linked with
values of 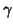 and the sample size
and the sample size 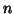 . Roughly speaking when
. Roughly speaking when 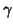 is close to
is close to 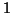 one
would need an
one
would need an 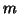 very close to
very close to 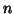 and so a large
and so a large 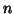 to achieve some gain in performing a
conjunction of only
to achieve some gain in performing a
conjunction of only 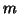 .
.


Next: Variance ratio smoothing
Up: Alternatives to the Random
Previous: Alternatives to the Random
Didier Leibovici
2001-03-01