

Next: Finite Mixture Model
Up: Segmentation of Brain MR
Previous: Introduction
Hidden Markov Random Field Model
Let
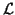 and
and
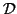 be two alphabets:
be two alphabets:
Let
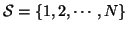 be the set of indices and
be the set of indices and
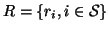 denote any family of random variables
indexed by
denote any family of random variables
indexed by
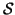 ,
in which each random variable Ri takes
a value zi in its state space. Such a family R is called a
random field. The joint event
,
in which each random variable Ri takes
a value zi in its state space. Such a family R is called a
random field. The joint event
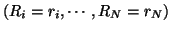 is
simplified to R=r where
is
simplified to R=r where
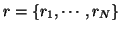 is a
configuration of R, corresponding to a realization of
this random field. Let X and Y be two such random fields whose
state spaces are
is a
configuration of R, corresponding to a realization of
this random field. Let X and Y be two such random fields whose
state spaces are
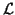 and
and
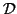 respectively so
that for
respectively so
that for
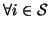 we have
we have
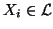 and
and
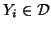 .
Let x denote a configuration
of X and
.
Let x denote a configuration
of X and
 be the set of all possible configurations
so that
be the set of all possible configurations
so that
Similarly, let y be a configuration of Y and
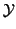 be the set of all possible configurations so that
be the set of all possible configurations so that
Given 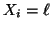 ,
Yi follows a conditional probability
distribution
,
Yi follows a conditional probability
distribution
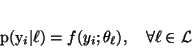 |
(1) |
where
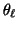 is the set of parameters. For all
is the set of parameters. For all 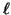 ,
the
function family
,
the
function family
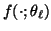 has the same known analytic
form. We also assume that (X, Y) is pairwise independent,
meaning
has the same known analytic
form. We also assume that (X, Y) is pairwise independent,
meaning
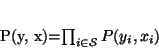 |
(2) |
In order to develop the HMRF model we firstly take the standard FM
model as a comparison.


Next: Finite Mixture Model
Up: Segmentation of Brain MR
Previous: Introduction
Yongyue Zhang
2000-05-11