++++ PTA- 3 modes ++++
data= J12.gm16 576 100 12
just slice 16
------Percent Rebuilt---- 23.34021%
------Percent Rebuilt from Selected ---- 17.01323%
-no- --Sing Val-- --ssX-- --local Pct-- --Global Pct--
vs111 1 191.376 599772 6.1064 6.1064
576 vs111 100 12 3 85.062 70189 10.3088 1.2064
100 vs111 576 12 6 97.382 81266 11.6694 1.5812
100 vs111 576 12 7 87.138 81266 9.3434 1.2660
12 vs111 576 100 9 87.616 80815 9.4988 1.2799
vs222 11 133.299 440752 4.0314 2.9625
vs333 21 97.991 370027 2.5950 1.6010
12 vs333 576 100 29 77.825 42284 14.3237 1.0098
++++ ++++
Shown are selected over 21 PT with var> 1% total
| 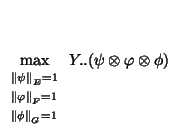
![\includegraphics[width=15cm]{rgm16.vs111.ps}](img18.gif)
![\includegraphics[width=15cm]{rgm16.vs222.ps}](img29.gif)