

Next: Increasing the Complexity -
Up: Local Parameter Estimation: Theory
Previous: Local Parameter Estimation: Theory
A Simple Partial Volume Model.
Here we take a slightly different approach to modeling in
DWMRI. Instead of modeling the diffusion shape directly, we attempt
to build a model of the underlying fibre structure which predicts the
diffusion shape, and hence the MR measurements. The simplest such
model of fibre structure is to assume that all fibers pass through a
voxel in the same direction. Assuming no diffusion-diffusion exchange,
this leads to a simple two compartment partial volume model. The first
compartment models diffusion in and around the axons, with diffusion
only in the fibre direction. The second models the diffusion of free
water in the voxel as isotropic. One consequence of this model is
that the diffusivity (and hence the restriction to water diffusion)
in all directions perpendicular to the fibre axis is constrained to be
the same. This is very different to the Diffusion Tensor model, where
any ellipsoidal diffusion shape may be modeled.
The predicted diffusion signal is
where 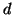 is the diffusivity,
is the diffusivity, 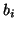 and
and 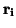 are the b-value
and gradient direction associated with the
are the b-value
and gradient direction associated with the
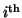 acquisition,
acquisition, 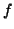 and
and
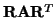 are the fraction of
signal contributed by, and anisotropic diffusion tensor along, the
fibre direction
are the fraction of
signal contributed by, and anisotropic diffusion tensor along, the
fibre direction
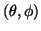 . That is
. That is 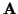 is fixed as:
is fixed as:
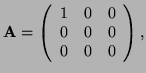 |
(13) |
and 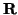 rotates
rotates 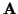 to
to
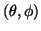 :
:
Again noise is modeled as 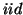 Gaussian:
Gaussian:
where the parameter set 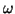 now has 6 free parameters
(
now has 6 free parameters
(
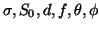 ). Each of these parameters is subject
to a prior distribution, which are chosen to be non-informative except
for where we ensure positivity:
). Each of these parameters is subject
to a prior distribution, which are chosen to be non-informative except
for where we ensure positivity:


Next: Increasing the Complexity -
Up: Local Parameter Estimation: Theory
Previous: Local Parameter Estimation: Theory
Tim Behrens
2004-01-22
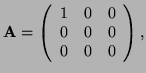
![]() Gaussian:
Gaussian: