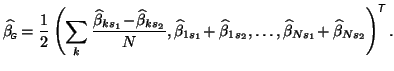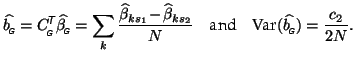

Next: Numerical simulation
Up: Examples
Previous: Repeated Measures
Let us assume that for each of  subject there exist two measurements obtained under different conditions
subject there exist two measurements obtained under different conditions 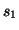 ,
, 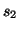 and that we are interested in the significance of the mean group difference
and that we are interested in the significance of the mean group difference
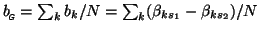 . We will assume that the between-subject variance and the between-session variance is equal across subjects and conditions. Note that this is a notational simplification within this framework which might or might not become a necessary condition once we try to estimate the associated group-level parameters.
Similar to the previous sections, we model this as
. We will assume that the between-subject variance and the between-session variance is equal across subjects and conditions. Note that this is a notational simplification within this framework which might or might not become a necessary condition once we try to estimate the associated group-level parameters.
Similar to the previous sections, we model this as
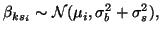
and
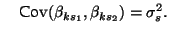
Let
where, again,
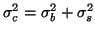 and where the group design matrix,
and where the group design matrix,
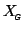 , de-means the first level estimates for each subject. Assume for simplicity that
, de-means the first level estimates for each subject. Assume for simplicity that
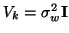 ,
,
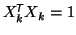 and define
and define
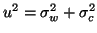 . Then
. Then
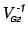 will be block diagonal with blocks of
Furthermore, let
will be block diagonal with blocks of
Furthermore, let
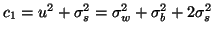 and
and
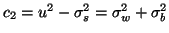 . Then
. Then
so that
Using
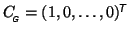 , the group parameter estimate writes as
As expected, the variance of the group level estimate no longer depends on the between-subject variance
, the group parameter estimate writes as
As expected, the variance of the group level estimate no longer depends on the between-subject variance
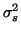 . Note that this approach is equivalent to using a three level approach with an unpaired
. Note that this approach is equivalent to using a three level approach with an unpaired 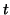 -test of de-meaned repeated measures.
-test of de-meaned repeated measures.
Subsections


Next: Numerical simulation
Up: Examples
Previous: Repeated Measures
Christian Beckmann
2003-07-16
![\begin{displaymath}
V=\left[
\begin{array}{ccc}
V_1& & 0 \\
& \ddots & \\
0...
... & & & \! 1 \\
\!\!-\!1 & & & & \! 1 \\
\end{array}\right],
\end{displaymath}](img186.png)
![$\displaystyle \widetilde{U}^{\mbox{\scriptsize\textit{\sffamily {-1}}}}=\frac{1...
...}=\left[\begin{array}{cc}
u^2&\sigma_s^2\\
\sigma_s^2&u^2
\end{array}\right].
$](img191.png)
![\begin{displaymath}
X_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{\scriptsiz...
.../N &&&\\
&c_1 && \\
&&\ddots &\\
&&&c_1
\end{array}\right],
\end{displaymath}](img194.png)