

Next: Inference
Up: Model
Previous: Model
Two-level GLM
Consider an experiment where there are 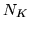 first-level sessions
and that for each first-level session,
first-level sessions
and that for each first-level session, 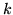 , the preprocessed FMRI
data is a
, the preprocessed FMRI
data is a 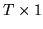 vector
vector 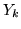 , the
, the
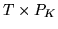 design
matrix is
design
matrix is 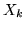 , and
, and 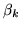 is a
is a
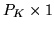 vector of
parameter estimates (
vector of
parameter estimates (
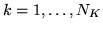 ). The preprocessed FMRI
data,
). The preprocessed FMRI
data, 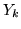 , is assumed to have been
prewhitened (25,4). An individual GLM
relates first-level parameters to the
, is assumed to have been
prewhitened (25,4). An individual GLM
relates first-level parameters to the 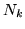 individual data sets:
individual data sets:
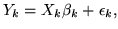 |
|
|
(1) |
where
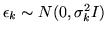 . In this paper we
consider the variance components as unknown with the exception of
the first-level FMRI time-series autocorrelation. The residuals
. In this paper we
consider the variance components as unknown with the exception of
the first-level FMRI time-series autocorrelation. The residuals
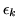 are assumed to be prewhitened data and as a result
are uncorrelated. This inherently means that we assume that the
autocorrelation is known with no uncertainty, an assumption which
is commonly made in FMRI time-series
analysis (8,25,4). Note that the
first level design matrices,
are assumed to be prewhitened data and as a result
are uncorrelated. This inherently means that we assume that the
autocorrelation is known with no uncertainty, an assumption which
is commonly made in FMRI time-series
analysis (8,25,4). Note that the
first level design matrices, 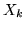 , do not need to be the same for
all
, do not need to be the same for
all 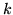 .
.
Using the block diagonal forms, i.e. with
![$\displaystyle Y\! =\! \left[\! \begin{array}{c} Y_1 \\ Y_2 \\ \vdots \\ Y_{N_K}...
...begin{array}{c} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_{N_K}
\end{array} \right]$](img20.png)
and
![$\displaystyle \quad
\epsilon\! =\! \left[\! \begin{array}{c} \epsilon_1 \\ \epsilon_2
\\ \vdots \\ \epsilon_{N_K}
\end{array}\! \right]
$](img21.png)
the two-level model is
where 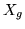 is the
is the
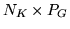 second-level design matrix
(e.g. separating controls from normals or modelling different
sessions for subjects),
second-level design matrix
(e.g. separating controls from normals or modelling different
sessions for subjects), 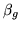 is the
is the
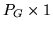 vector of
second-level parameters, and
vector of
second-level parameters, and
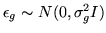 and where
and where
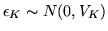 with
with 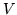 denoting the
diagonal form of first-level covariance matrices
denoting the
diagonal form of first-level covariance matrices
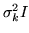 .
We call
.
We call
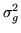 the random effects variance.
the random effects variance.


Next: Inference
Up: Model
Previous: Model
![]() first-level sessions
and that for each first-level session,
first-level sessions
and that for each first-level session, ![]() , the preprocessed FMRI
data is a
, the preprocessed FMRI
data is a ![]() vector
vector ![]() , the
, the
![]() design
matrix is
design
matrix is ![]() , and
, and ![]() is a
is a
![]() vector of
parameter estimates (
vector of
parameter estimates (
![]() ). The preprocessed FMRI
data,
). The preprocessed FMRI
data, ![]() , is assumed to have been
prewhitened (25,4). An individual GLM
relates first-level parameters to the
, is assumed to have been
prewhitened (25,4). An individual GLM
relates first-level parameters to the ![]() individual data sets:
individual data sets:
![$\displaystyle Y\! =\! \left[\! \begin{array}{c} Y_1 \\ Y_2 \\ \vdots \\ Y_{N_K}...
...begin{array}{c} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_{N_K}
\end{array} \right]$](img20.png) and
and![$\displaystyle \quad
\epsilon\! =\! \left[\! \begin{array}{c} \epsilon_1 \\ \epsilon_2
\\ \vdots \\ \epsilon_{N_K}
\end{array}\! \right]
$](img21.png)