Please send feedback to steve@fmrib.ox.ac.uk
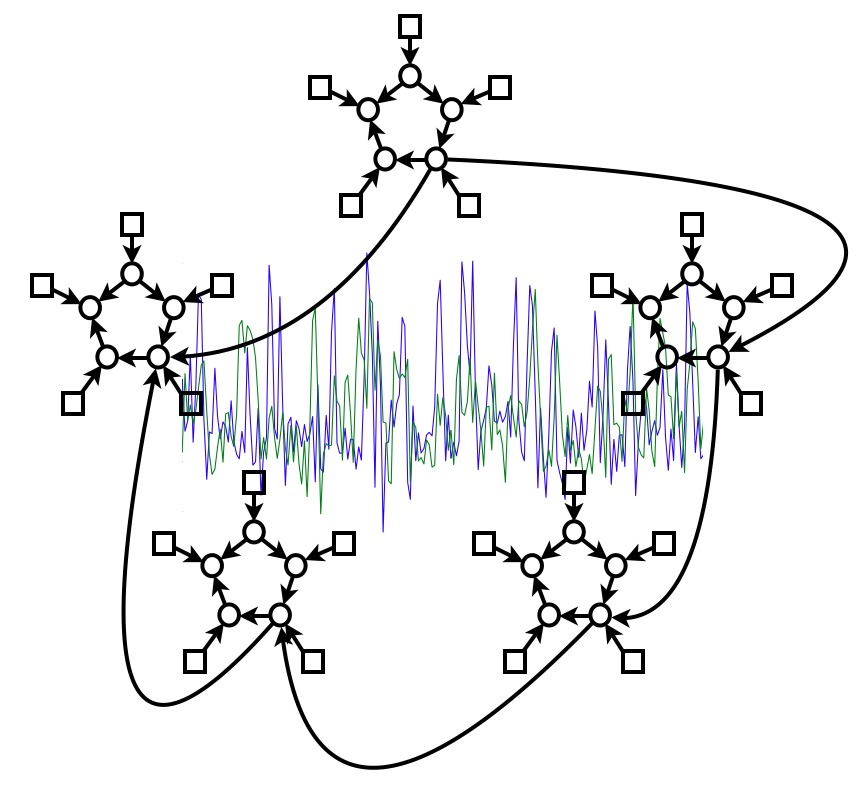
There is great interest in estimating brain "networks" from FMRI data. This is often attempted by identifying a set of functional "nodes" (e.g., spatial ROIs or ICA maps) and then conducting a connectivity analysis between the nodes, based on the FMRI timeseries associated with the nodes. Analysis methods range from very simple measures that consider just two nodes at a time (e.g., correlation between two nodes' timeseries) to sophisticated approaches that consider all nodes simultaneously and estimate one global network model (e.g., Bayes net models). Many different methods are being used in the literature, but almost none has been carefully validated or compared for use on FMRI timeseries data. In this work we generate rich, realistic simulated FMRI data for a wide range of underlying networks, experimental protocols and problematic confounds in the data, in order to compare different connectivity estimation approaches. Our results show that in general correlation-based approaches can be quite successful, methods based on higher-order statistics are less sensitive, and lag-based approaches perform very poorly. More specifically: there are several methods that can give high sensitivity to network connection detection on good quality FMRI data, in particular, partial correlation, regularised inverse covariance estimation and several Bayes net methods; however, accurate estimation of connection directionality is more difficult to achieve, though Patel's τ can be reasonably successful. With respect to the various confounds added to the data, the most striking result was that the use of functionally inaccurate ROIs (when defining the network nodes and extracting their associated timeseries) is extremely damaging to network estimation; hence, results derived from inappropriate ROI definition (such as via structural atlases) should be regarded with great caution.
The work has been published in NeuroImage.
The BOLD timeseries data and underlying ground-truth network matrices are available below. We welcome any feedback on our evaluation paper or the simulation datasets. The data from all 28 simulations is available here (slightly improved as of 24/08/2012) in MATLAB format. The variables are:
To view the mean (across 50 "subjects") ground truth network:
imagesc(squeeze(mean(net)));
To get the matrix of all nodes' timeseries for just the first subject:
ts1=ts(1:Ntimepoints,:);
To see the (full, normalised) correlation matrix for just the first subject:
imagesc(corrcoef(ts1))
To get the partial correlation matrix for just the first subject:
ic=-inv(cov(ts1)); % raw negative inverse covariance matrix
r=(ic ./ repmat(sqrt(abs(diag(ic))),1,Nnodes)) ./ repmat(sqrt(abs(diag(ic)))',Nnodes,1); % use diagonal to get normalised coefficients
r=r+eye(Nnodes); % remove diagonal
To run ICOV and convert to normalised coefficients, first grab the L1precision code, and then::
lambda=5; % arbitrary choice of regularisation!
oc=cov(ts1); % raw covariance
ic=-L1precisionBCD(oc/mean(diag(oc)),lambda/1000); % get regularised negative inverse covariance
r=(ic ./ repmat(sqrt(abs(diag(ic))),1,Nnodes)) ./ repmat(sqrt(abs(diag(ic)))',Nnodes,1); % use diagonal to get normalised coefficients
r=r+eye(Nnodes); % remove diagonal