Statistical inference

The set of voxels exceeding some threshold $u$ comprises $m$ clusters each of $n$ voxels. The expectations of $m$, $n$ and the total number of voxels above threshold, $N$, are related

$$E\{N\} = E\{m\} \cdot E\{n\}.$$ (1)

For our purposes we can calculate all the necessary information knowing $E\{m\}$ and this can be approximated by

$$E\{m\} \approx V(2\pi)^{-2}\vert\Lambda\vert^{1/2}(t^2-1)e^{-{t^2}/{2}},$$ (2)

where $W$ is an estimate of the smoothness of the GRF, $D$ the number of dimensions in the GRF and $S$ is the number of in-brain voxels.

The probability of $c$ clusters in this excursion set is approximated by a Poisson

$$P(m = c) \approx \lambda(c, E\{m\})$$ (3)

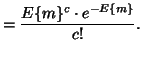$$= \frac{E\{m\}^c \cdot e^{-E\{m\}}}{c!}.$$ (4)

The number of voxels $n$ comprising a cluster is distributed according to

$$P(n \ge k) \approx e^{-\beta k^{{2}/{D}}},$$ (5)

where

$$\beta = \left[\frac{\Gamma\left(\frac{D}{2} +1\right) E\{m\}} {\left(S\cdot\Phi(-u)\right)}\right]^\frac{2}{D}.$$ (6)

We can calculate $P(n_{max} \ge k)$ [3] by calculating the product of $P(n = m)$ and $1 - P(n < k)$ summed over $m$

$$P(n_{max} \ge k) = \sum_{i=1}^{\infty} P(m = i) \cdot [ 1 - P(n < k)^{i} ]$$ (7)

$$= 1 - \exp \left( -E\{m\} \cdot P( n \ge k ) \right)$$ (8)

$$= 1 - \exp \left( -E\{m\} e^{-\beta k^{{2}/{D}}} \right).$$ (9)