

Next: A more robust smoothness
Up: Smoothness estimation
Previous: Smoothness estimation
Smoothness a la SPM
The current implementations of SPM (SPM99) use the smoothness
estimation as described in Kiebel et al [5].
For a Gaussian random field the smoothness is defined as
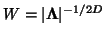 where
where 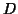 is the dimensionality
of the field and
is the dimensionality
of the field and
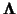 the covariance matrix of it's
first partial derivatives. An unbiased estimator for the covariance of
the partial derivatives is given by
the covariance matrix of it's
first partial derivatives. An unbiased estimator for the covariance of
the partial derivatives is given by
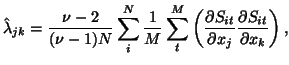 |
(10) |
where 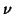 is the number of degrees of freedom,
is the number of degrees of freedom, 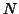 the number of
voxel positions (
the number of
voxel positions (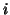 ) and
) and 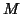 the number of time points (
the number of time points (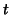 ) in a FMRI time series. In fact we don't have to evaluate this equation for the
whole covariance matrix. The off-diagonal elements will be zero so we
only need to calculate the diagonal elements of
) in a FMRI time series. In fact we don't have to evaluate this equation for the
whole covariance matrix. The off-diagonal elements will be zero so we
only need to calculate the diagonal elements of
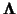
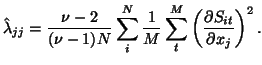 |
(11) |
The partial derivative is evaluated via the gradient operator
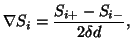 |
(12) |
for non-edge voxels, where 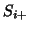 and
and 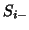 are
are 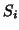 s
neighbouring voxels in the dimension along which the derivative is
currently being evaluated.
s
neighbouring voxels in the dimension along which the derivative is
currently being evaluated.
Now we can calculate the FWHM of the theoretical Gaussian responsible
for the observed smoothness
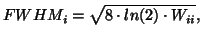 |
(13) |
where 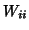 is the variance,
is the variance, 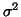 , of the Gaussian
point-spread-function computed from the covariance measure for the
, of the Gaussian
point-spread-function computed from the covariance measure for the
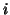 th dimension
th dimension
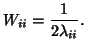 |
(14) |
A combined value for the FWHM is given by the geometric mean of the
various FWHM
![$\displaystyle FWHM = \left[\prod_{i=0}^{D}FWHM_i\right]^{1/D}.$](img43.gif) |
(15) |


Next: A more robust smoothness
Up: Smoothness estimation
Previous: Smoothness estimation
David Flitney
2001-11-29
![]() where
where ![]() is the dimensionality
of the field and
is the dimensionality
of the field and
![]() the covariance matrix of it's
first partial derivatives. An unbiased estimator for the covariance of
the partial derivatives is given by
the covariance matrix of it's
first partial derivatives. An unbiased estimator for the covariance of
the partial derivatives is given by
![]()