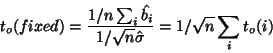Next: Random Subject Analysis
Up: Multi-subject analysis
Previous: Multi-subject analysis
Following the assumption that each subject's estimated activation
parameters are taken from the distributions:
the population mean activation by 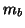 is estimated
is estimated
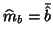 with the following distribution
with the following distribution
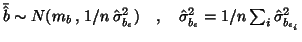 .
.
Now, testing 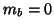 (null
hypothesis) is a one sample
(null
hypothesis) is a one sample 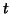 -test:
-test:
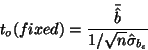 |
(4) |
Note that deciding that the
pooled variance is a ``better'' estimate of single-subject variance, that is, for every  ,
,
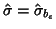 then:
then:
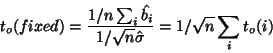 |
(5) |
This simplified fixed-effects analysis is therefore
virtually identical to the ``Group Z'' method:
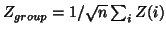 .
The main shortcoming of the fixed-effects approach is that it
considers the errors of measurement estimated for the subjects as
the only source of variation when estimating the population mean.
That is to say, only within-subject variation is accounted for. No
consideration of between-subject variation is considered;
therefore it is valid only for the subjects chosen in this
experiment (no sampling variation). Put another way, when looking
at variation of an activation, it has to account for variation
during the experiment on a subject (between measures or
within-subject) and the choice of subjects (between subject).
.
The main shortcoming of the fixed-effects approach is that it
considers the errors of measurement estimated for the subjects as
the only source of variation when estimating the population mean.
That is to say, only within-subject variation is accounted for. No
consideration of between-subject variation is considered;
therefore it is valid only for the subjects chosen in this
experiment (no sampling variation). Put another way, when looking
at variation of an activation, it has to account for variation
during the experiment on a subject (between measures or
within-subject) and the choice of subjects (between subject).



Next: Random Subject Analysis
Up: Multi-subject analysis
Previous: Multi-subject analysis
Didier Leibovici
2001-03-01