The objective is to find an expansion of equation 1 for
large values of ![]() . In this case a Taylor expansion will not be useful.
The solution is found using an integral recurrence relation.
. In this case a Taylor expansion will not be useful.
The solution is found using an integral recurrence relation.
Consider the integral:
| (8) |
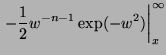 |
(9) | ||
| (10) |
Now if ![]() then
then
![]() . Therefore, for large Z, this
enables the error function (related to
. Therefore, for large Z, this
enables the error function (related to ![]() ) to be expanded in terms of
) to be expanded in terms of
![]() where the absolute values of
where the absolute values of ![]() continue to decrease as
continue to decrease as ![]() increases.
Specifically:
increases.
Specifically:
| (11) | |||
| (12) | |||
| (13) |
Equations 2 and 1, and the fact that
![]() can be used to relate
can be used to relate ![]() and
and ![]() , giving:
, giving:
| (15) |
Therefore by taking the logarithm, and neglecting the ![]() term, the
asymptotic expansion for the Z statistic is:
term, the
asymptotic expansion for the Z statistic is: