In this case the intersection of the volume domains becomes small and
generally any tissue in one volume corresponds only to background in
the other volume. More specifically, consider the case where there is
a single, small amount of tissue contained in either volume, with the
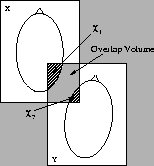
proportion of voxels containing tissue to total number of voxels in
the intersection volume being ![]() for X and
for X and ![]() for Y(see also figure 1). Furthermore, without loss
of generality, take the background intensity as zero and the tissue
intensity as B. The cost functions are then given by:
for Y(see also figure 1). Furthermore, without loss
of generality, take the background intensity as zero and the tissue
intensity as B. The cost functions are then given by:
| CW | 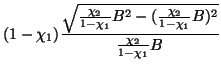 |
||
| (17) | |||
| (18) | |||
| CCR | 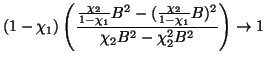 |
||
| (19) | |||
| CJE | = | ||
| (20) | |||
| CMI | = | H(X,Y) - H(X) - H(Y) | |
| (21) | |||
| CNMI | = | 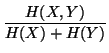 |
|
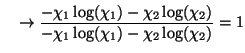 |
|||
| (22) |
 |
Thus the Woods function (as
![]() )
and Joint Entropy
actually approach the minimum values which indicates, erroneously,
that the registration is good. The other three cost functions
approach their maximum values, indicating poor registrations.
)
and Joint Entropy
actually approach the minimum values which indicates, erroneously,
that the registration is good. The other three cost functions
approach their maximum values, indicating poor registrations.