| Translation: | (28) | ||
| Rotation: | 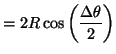 |
(29) | |
| Scale: | (30) | ||
| Skew: | (31) |
A major component in the overall optimisation process is the local optimisation method. This local optimisation is called repeatedly and so should be efficient. Here Powell's method was chosen since it is a commonly used and efficient local optimisation method [Press et al., 1995].
The changes in transformation used by the optimisation method should
also be adapted to the resolution of the volumes. For example,
computing very small changes in transformation when the voxel size is
large corresponds to very small sub-voxel changes and is a waste of
computation. Consequently, a lower limit for the transformation step
size is enforced. This step size is easily calculated by imposing the
condition that the maximum voxel position shift should be less than
half a voxel. More precisely, with a brain of radius R, and an
origin located at the centre of mass for the brain, the maximum shifts
are:
| Translation: | (28) | ||
| Rotation: | 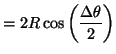 |
(29) | |
| Scale: | (30) | ||
| Skew: | (31) |
For cubic voxels of side-length n mm the constraint becomes
![]() which gives:
which gives:
| (32) | |||
| (33) | |||
| (34) | |||
| (35) |
For n=1 mm this gives
![]() mm,
mm,
![]() ,
,
![]() and
and
![]() .
However, since the voxel shift
due to translation is constant across the volume, whereas all others are
less towards the centre, it pays to be more conservative for
.
However, since the voxel shift
due to translation is constant across the volume, whereas all others are
less towards the centre, it pays to be more conservative for ![]() .
.
Given these lower limits on the parameter steps, Powell's algorithm is modified by changing the termination conditions so that when the 1D optimisation (Brent's method) has bounded the minimum within an interval that is less than one parameter step, then it returns the mid-point of the current interval. In this way, significant savings in computation can be had without any sacrifice in accuracy. Moreover, accuracy is largely determined on the final pass, which can have even more conservative bounds if better accuracy is required.