The task is to find a statistic that will estimate the smoothing
parameters of a Gaussian Random Field. Such a field can be
constructed by taking an uncorrelated, zero-mean (white-noise) field,
![]() , and smoothing it spatially with a Gaussian filter. That is,
the smoothed field
, and smoothing it spatially with a Gaussian filter. That is,
the smoothed field ![]() is given by:
is given by:
| (1) |
| (2) | |||
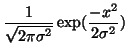 |
(3) |
In addition, the auto-correlation of ![]() is:
is:
| (4) |