| (42) |
As the approximation of the derivative (equation 40) is not precise, it introduces a bias into the SPM estimation technique. This source of bias can be eliminated by using a finite difference calculation instead of the derivative-based one.
That is, the difference field is:
| (42) |
The variance of this difference field is:
| (43) | |||
| (44) |
Setting
![]() with
with
![]() ,
the expectations can be calculated using equation 14:
,
the expectations can be calculated using equation 14:
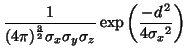 |
(45) | ||
| (46) |
| (47) |
This enables the individual smoothing parameters,
![]() to be found. That is:
to be found. That is: