Model Equivalence

Theorem:

The two-level model specified by equations 1 and 6 is fully equivalent to the single-level model specified by equation 4 in terms of both modelling and estimation when

$$V_{\mbox{\tiny\textit{\sffamily {$\!$G2}}}}^{\mbox{}}= V_{\mbox{\... ...iptsize\textit{\sffamily {-1}}}}X)^{\mbox{\scriptsize\textit{\sffamily {-1}}}}.$$ (10)

That is, the second-level covariance is set as the sum of the group-covariance from the single-level model and the first-level parameter covariance from the two-level model.

Proof:

We employ the Sherman-Morrison-Woodbury formula (equation 17 from the appendix)

to write $W^{\mbox{\scriptsize\textit{\sffamily {-1}}}}$ as

$$W^{\mbox{\scriptsize\textit{\sffamily {-1}}}}=V^{\mbox{\scriptsiz... ...tsize\textit{\sffamily {$\!$T}}}}V^{\mbox{\scriptsize\textit{\sffamily {-1}}}},$$ (11)

and let

$$Q = (X^{\mbox{\scriptsize\textit{\sffamily {$\!$T}}}}V^{\mbox{\scriptsize\textit{\sffamily {-1}}}}X)^{\mbox{\scriptsize\textit{\sffamily {-1}}}},$$

which is the covariance estimate for the $\widehat{\beta}$s, from equation 5.

Then

$$X^{\mbox{\scriptsize\textit{\sffamily {$\!$T}}}}W^{\mbox{\scriptsize\textit{\sffamily {-1}}}}X = \left({\mathbf {I}}-\left(V_{\mbox{\tiny\textit{\sffamily {$\!$G}... ...ze\textit{\sffamily {-1}}}}\right)Q^{\mbox{\scriptsize\textit{\sffamily {-1}}}}$$

$$= \left(V_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}+Q\right)^{\mbox{\scriptsize\textit{\sffamily {-1}}}},$$

by using equation 17 again, and

$$X^{\mbox{\scriptsize\textit{\sffamily {$\!$T}}}}W^{\mbox{\scripts... ...tsize\textit{\sffamily {$\!$T}}}}V^{\mbox{\scriptsize\textit{\sffamily {-1}}}}.$$

Inserting this into equation 8 gives

$$\widehat{\beta_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}} = \left(X_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{\scriptsi... ...size\textit{\sffamily {$\!$T}}}}V^{\mbox{\scriptsize\textit{\sffamily {-1}}}}Y,$$

$$\textrm{Cov}(\widehat{\beta_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}}) = \left(X_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{\scriptsi... ...family {$\!$G}}}}^{\mbox{}}\right)^{\mbox{\scriptsize\textit{\sffamily {-1}}}},$$

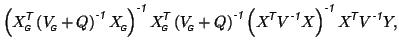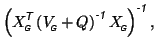which becomes equivalent to equation 9 if

$$V_{\mbox{\tiny\textit{\sffamily {$\!$G2}}}}^{\mbox{}}=V_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}+Q.$$

$\Box$

For this choice of $V_{\mbox{\tiny\textit{\sffamily {$\!$G2}}}}^{\mbox{}}$, the group-level parameter estimates can be written as

$$\widehat{\beta_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}... ...{\mbox{}}+Q\right)^{\mbox{\scriptsize\textit{\sffamily {-1}}}}\widehat{\beta},$$

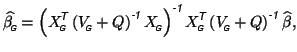
that is, they become a function of the first-level parameter estimates $\widehat{\beta}$ and their associated covariances $Q = \left(X^{\mbox{\scriptsize\textit{\sffamily {$\!$T}}}} V^{\mbox{\scriptsize\textit{\sffamily {-1}}}}X\right)^{\mbox{\scriptsize\textit{\sffamily {-1}}}}$ only.

Note that by simply applying this theorem multiple times, these results extend to any multi-level GLM. For example, one can calculate parameter estimates for groups of groups using a multi-level approach by only keeping track of parameter estimates and associated covariances at each level. Note also that parts of this proof can simply be obtained by characterising the necessary conditions on sufficient statistics for $\beta_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}$ [16].