

Next: Simple Problem Formulation
Up: tr01mj2
Previous: Introduction
Let the individual voxel time courses be arranged in a matrix, 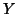 ,
such that each column represents a single voxel time course, and each
row represents a spatial image (at a fixed time point). That is,
,
such that each column represents a single voxel time course, and each
row represents a spatial image (at a fixed time point). That is, 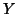 is a
is a
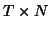 matrix where
matrix where 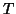 is the number of time points, and
is the number of time points, and
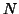 is the number of voxels, where we assume
is the number of voxels, where we assume 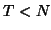 so that spatial
ICA is being performed.
so that spatial
ICA is being performed.
The matrix is then preprocessed to:
- remove the mean spatial map
(the average of all the rows of
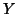 ) from each row of
) from each row of 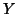 ;
;
- (optional) normalise the variance of each individual
time course (each column of
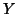 set to have unit variance);
set to have unit variance);
- remove the mean time course (the average of all the columns of
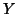 ) from
each column of
) from
each column of 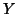 .
.
With this data, a general ICA decomposition can be written as
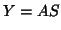 |
(1) |
where 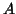 is a
is a
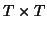 matrix of time courses and
matrix of time courses and 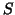 is a
is a
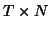 matrix of spatial maps which are pairwise independent
in a statistical sense. Note that the
matrix of spatial maps which are pairwise independent
in a statistical sense. Note that the 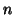 th row of
th row of
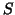 is a spatial map that is associated with the
is a spatial map that is associated with the 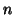 th column of
th column of 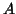 (a time course).
(a time course).
Subsections


Next: Simple Problem Formulation
Up: tr01mj2
Previous: Introduction
Stephen Smith
2001-11-29
![]() ,
such that each column represents a single voxel time course, and each
row represents a spatial image (at a fixed time point). That is,
,
such that each column represents a single voxel time course, and each
row represents a spatial image (at a fixed time point). That is, ![]() is a
is a
![]() matrix where
matrix where ![]() is the number of time points, and
is the number of time points, and
![]() is the number of voxels, where we assume
is the number of voxels, where we assume ![]() so that spatial
ICA is being performed.
so that spatial
ICA is being performed.