

Next: Multi-Start Optimisation with Perturbations
Up: A Global-Local Hybrid Optimisation
Previous: Local Optimisation
To estimate the final transformation sufficiently accurately, a
brute-force search of the transformation space is infeasible, even for
rigid-body transformations. However, at the lowest resolution (8mm scale)
only the gross image features still exist and so a coarse search of the
cost function at this resolution should reflect the major changes
in rotation, translation and global scaling, allowing large mis-registrations
to be avoided.
Speed remains an issue, even for coarse searches at low resolution.
Therefore, the search is restricted to the rotation parameters, as
these are the most difficult to find and are the cause of many large
mis-registrations. Furthermore, the search is divided into three
stages:
- a coarse search over the rotation parameters with a full local
optimisation of translation and global scale for each rotation
tried;
- a finer search over rotation parameters, but with only a single
cost function evaluation at each rotation (for efficiency);
- a full local optimisation (rotation, translation and global scale)
for each local minimum detected from the previous stage.
The first of these stages is straightforward. Given a set of
rotations to try (by default we use 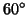 increments in each of
the Euler angles, leading to
increments in each of
the Euler angles, leading to 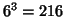 different rotations), the local
optimisation routine is called for the translation and global scale
only. That is, the rotation is left fixed, and the best translation
and global scale for this particular rotation is found. These results
are then stored for use in the later stages.
The second stage takes a larger set of rotations (by default we use
different rotations), the local
optimisation routine is called for the translation and global scale
only. That is, the rotation is left fixed, and the best translation
and global scale for this particular rotation is found. These results
are then stored for use in the later stages.
The second stage takes a larger set of rotations (by default we use
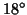 degree increments, leading to
degree increments, leading to
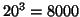 different rotations)
but only evaluates the cost function once for each rotation. This
contrasts with the previous stage where the cost function is typically
evaluated between 10 and 30 times during the local optimisation.
However, in order for the evaluation to be a reasonable estimate of the
best cost function with this rotation, the translation and global scale
parameters must be close to the optimal values. These parameter values
are supplied from the results of the previous stage, with the translation
parameters determined by interpolating between the stored translation values.
Global scale is fixed at the median global scale value over all the
stored values. This is done differently from the translation as the
scale should not vary greatly with rotation, whereas the translation
is highly coupled with the rotation values.
Finally, the third stage applies a full local optimisation, allowing
rotation to vary, at each local minimum detected from the results of
the previous stage. These local minima are defined as rotations where
the cost value found is less than for any of the ``neighbouring''
rotation values. There are often several such local minima, and
rather than force the selection of the best one at this stage, they
are all optimised and passed onto the higher resolution stages.
Although it is unlikely that the first stage in this process will get
very close to the correct rotation, the second stage should get close
enough for the local optimisation in the last stage to give a good
estimate. Note that in most registration methods there is no
equivalent of this search and a single local optimisation is performed
with the starting point being no rotation, no translation and unity
scaling (the identity transformation). As this method examines many
more possible starting transformations, cannot do any worse than
these simple methods.
different rotations)
but only evaluates the cost function once for each rotation. This
contrasts with the previous stage where the cost function is typically
evaluated between 10 and 30 times during the local optimisation.
However, in order for the evaluation to be a reasonable estimate of the
best cost function with this rotation, the translation and global scale
parameters must be close to the optimal values. These parameter values
are supplied from the results of the previous stage, with the translation
parameters determined by interpolating between the stored translation values.
Global scale is fixed at the median global scale value over all the
stored values. This is done differently from the translation as the
scale should not vary greatly with rotation, whereas the translation
is highly coupled with the rotation values.
Finally, the third stage applies a full local optimisation, allowing
rotation to vary, at each local minimum detected from the results of
the previous stage. These local minima are defined as rotations where
the cost value found is less than for any of the ``neighbouring''
rotation values. There are often several such local minima, and
rather than force the selection of the best one at this stage, they
are all optimised and passed onto the higher resolution stages.
Although it is unlikely that the first stage in this process will get
very close to the correct rotation, the second stage should get close
enough for the local optimisation in the last stage to give a good
estimate. Note that in most registration methods there is no
equivalent of this search and a single local optimisation is performed
with the starting point being no rotation, no translation and unity
scaling (the identity transformation). As this method examines many
more possible starting transformations, cannot do any worse than
these simple methods.


Next: Multi-Start Optimisation with Perturbations
Up: A Global-Local Hybrid Optimisation
Previous: Local Optimisation
Peter Bannister
2002-05-03