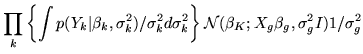

Next: Fast Approximation Point Estimates
Up: Appendix
Previous: Determining Reference Priors
Marginalising over
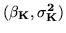 in the two-level model
in the two-level model
From the two-level model the full joint posterior distribution is
(equation 12):
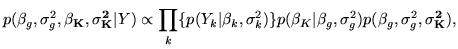 |
|
|
(36) |
where the prior is the reference prior for this full two-level
model (equation 13):
If we marginalise out
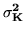 then we get:
then we get:
and then substitute in the summary result of the first-level model
in isolation (equation 10):
We can represent a multivariate non-central t-distribution using a
two-parameter Gamma distribution and a multivariate Normal
distribution (see appendix 10.3). This is achieved by
introducing a parameter 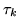 for each vector
for each vector 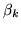 :
:
Writing
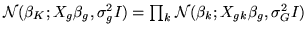 , where
, where 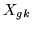 is the
is the 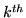 row vector of the second-level design matrix
row vector of the second-level design matrix
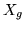 , we can now easily integrate out
, we can now easily integrate out 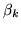 for all
for all 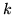 to
give:
to
give:
where
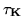 is a
is a
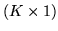 vector of the variables
vector of the variables
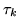 for
for
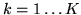 .
.


Next: Fast Approximation Point Estimates
Up: Appendix
Previous: Determining Reference Priors