

Next: Two-level
Up: Inference
Previous: Priors and Reference Analysis
First-level
Here we consider the first-level in isolation and derive the marginal
posterior distribution for 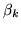 , the vector of GLM height
parameters for the first-level model fit.
Equation 1 gives us the likelihood for a
first-level model in isolation,
, the vector of GLM height
parameters for the first-level model fit.
Equation 1 gives us the likelihood for a
first-level model in isolation,
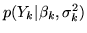 . The joint
posterior on all parameters in this model is then:
. The joint
posterior on all parameters in this model is then:
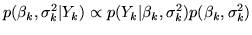 |
|
|
(8) |
where
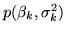 is the prior distribution on the
regression and variance parameters. We use the Berger-Bernardo
reference prior (see section 3.2), which is:
is the prior distribution on the
regression and variance parameters. We use the Berger-Bernardo
reference prior (see section 3.2), which is:
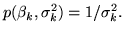 |
|
|
(9) |
However, equation 8 does not give the
distribution of interest for inference. We would like to infer on
the posterior distribution on the activation height parameters
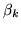 when the effect of estimating
when the effect of estimating
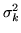 is accounted
for, i.e. we would like to infer on
is accounted
for, i.e. we would like to infer on
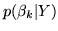 . To get this
distribution, we must marginalise the joint posterior (equation
8) over the parameter of no interest
. To get this
distribution, we must marginalise the joint posterior (equation
8) over the parameter of no interest
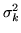 . This integral gives a multivariate non-central
t-distribution for the posterior distribution on
. This integral gives a multivariate non-central
t-distribution for the posterior distribution on
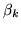 (18):
(18):
where
Note that if inference is performed in the frequentist framework,
the null distribution on 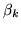 is the multivariate
central t-distribution with the exact same
covariance structure
is the multivariate
central t-distribution with the exact same
covariance structure
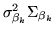 and
degrees of freedom,
and
degrees of freedom,
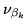 , and the maximum likelihood
estimate for
, and the maximum likelihood
estimate for 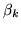 is exactly
is exactly
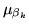 , the
mean of the posterior distribution in the Bayesian framework.
, the
mean of the posterior distribution in the Bayesian framework.


Next: Two-level
Up: Inference
Previous: Priors and Reference Analysis
![]() , the vector of GLM height
parameters for the first-level model fit.
Equation 1 gives us the likelihood for a
first-level model in isolation,
, the vector of GLM height
parameters for the first-level model fit.
Equation 1 gives us the likelihood for a
first-level model in isolation,
![]() . The joint
posterior on all parameters in this model is then:
. The joint
posterior on all parameters in this model is then: