

Next: Precision Parameter Hyperpriors
Up: Autoregressive Parameter Priors
Previous: Markov Random Field (MRF)
We are proposing to use a general order temporal AR model. The
difficulty with this is that different voxels require different
orders of temporal AR. The order varies between 0 and 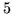 , but
with few voxels with order greater than
, but
with few voxels with order greater than
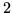 (43). Hence, we need some technique to allow the
model to automatically adjust to the required AR order at each
voxel.
Models with different order ARs have different number of
parameters, which is a well known problem for MCMC techniques. One
solution is to use reversible jumps (27) or jump
diffusion (39) which allow jumps between models of
different numbers of parameters. However, we can avoid this added
complexity by employing a technique used in Bayesian modelling
known as Automatic Relevance Determination (ARD) (36)
from the neural network literature. ARD requires the use of a
certain type of prior on a parameter whose relevance needs to be
determined. The simplest prior to use for this purpose is a
Gaussian with zero mean and precision
(43). Hence, we need some technique to allow the
model to automatically adjust to the required AR order at each
voxel.
Models with different order ARs have different number of
parameters, which is a well known problem for MCMC techniques. One
solution is to use reversible jumps (27) or jump
diffusion (39) which allow jumps between models of
different numbers of parameters. However, we can avoid this added
complexity by employing a technique used in Bayesian modelling
known as Automatic Relevance Determination (ARD) (36)
from the neural network literature. ARD requires the use of a
certain type of prior on a parameter whose relevance needs to be
determined. The simplest prior to use for this purpose is a
Gaussian with zero mean and precision 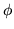 which is also to be
determined or sampled from. If the parameter in question is not
required then the precision
which is also to be
determined or sampled from. If the parameter in question is not
required then the precision 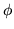 will be large, forcing the
parameter to be close to zero. The benefit of ARD is that any
unnecessary parameters are automatically forced to zero. The
disadvantage is that it makes it difficult to incorporate other
prior information at the same time as implementing ARD, and hence
in this work
the use of the ARD model excludes the use of the MRF prior of
equation 14. Note that we will also use the ARD
prior for automatic relevance determination of the HRF initial dip
and post-stimulus undershoot.
The prior for the temporal AR parameters is then:
will be large, forcing the
parameter to be close to zero. The benefit of ARD is that any
unnecessary parameters are automatically forced to zero. The
disadvantage is that it makes it difficult to incorporate other
prior information at the same time as implementing ARD, and hence
in this work
the use of the ARD model excludes the use of the MRF prior of
equation 14. Note that we will also use the ARD
prior for automatic relevance determination of the HRF initial dip
and post-stimulus undershoot.
The prior for the temporal AR parameters is then:
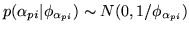 |
(15) |
The difference between this prior and the prior in
equation 13 is that here the precision,
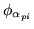 , is
an unknown hyperparameter and does itself have a hyperprior on it
(see next section), whereas in equation 13
the precision,
, is
an unknown hyperparameter and does itself have a hyperprior on it
(see next section), whereas in equation 13
the precision,
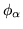 , is fixed at a small value. If there is information
in the data to support the existence of the parameter
, is fixed at a small value. If there is information
in the data to support the existence of the parameter
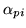 , then
, then
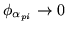 , else
, else
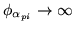 .
We also use ARD for the spatial AR parameters
.
We also use ARD for the spatial AR parameters
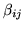 in the
spatially non-stationary model, to exclude spatial dependency
between voxels when it is not relevant.
in the
spatially non-stationary model, to exclude spatial dependency
between voxels when it is not relevant.


Next: Precision Parameter Hyperpriors
Up: Autoregressive Parameter Priors
Previous: Markov Random Field (MRF)