

Next: Spatial Mixture Modelling
Up: Artificial null data
Previous: Methods
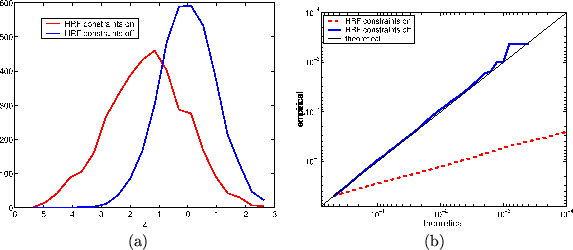
Figure 5(a) shows the histogram of
pseudo-z-statistics obtained for the two different models with and
without HRF constraints using the Variational Bayesian inference.
Figure 5(b) shows the log probability-log
probability plots. These show plots of (nominal/theoretical)
frequentist FPR against that obtained empirically.
The nominal/theoretical FPR is only applicable to the
unconstrained HRF model, as we then have noninformative priors and
we would expect the Bayesian inference to be equivalent to
frequentist inference. Accordingly, the log probability-log
probability plot shows good correspondence between the empirically
obtained probabilities under the tail for a given z-statistic, and
that which we expect from frequentist theory, for the
unconstrained HRF model.
Recall that to make the inference tractable under Variational
Bayes, we introduced a utility parameter,
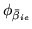 , which we update with point estimates an
approximation which may have effected the marginal posterior over
, which we update with point estimates an
approximation which may have effected the marginal posterior over
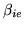 . The fact that we obtain good correspondence here
between our inference and the (for this model, known to be
correct) frequentist results provides some validation that the
marginal posterior over
. The fact that we obtain good correspondence here
between our inference and the (for this model, known to be
correct) frequentist results provides some validation that the
marginal posterior over 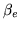 is not significantly
affected.
Unlike the unconstrained model, we would not expect the
constrained HRF model to give pseudo-z-statistics that conform to
frequentist theory. This is because we now have informative HRF
shape priors causing Bayesian inference to be different to
frequentist inference. The log probability-log probability plot
shows that we get probabilities under the tail for a given
z-statistic much smaller empirically than if the frequentist GLM
solution held true. The histogram in
figure 5(a) shows that this is due to a
large shift in the histogram to lower pseudo-z-statistics (the
mode is at about
is not significantly
affected.
Unlike the unconstrained model, we would not expect the
constrained HRF model to give pseudo-z-statistics that conform to
frequentist theory. This is because we now have informative HRF
shape priors causing Bayesian inference to be different to
frequentist inference. The log probability-log probability plot
shows that we get probabilities under the tail for a given
z-statistic much smaller empirically than if the frequentist GLM
solution held true. The histogram in
figure 5(a) shows that this is due to a
large shift in the histogram to lower pseudo-z-statistics (the
mode is at about 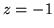 ). The HRF constraints reduce the power in
those voxels where the linear combinations of the basis functions
do not give sensible HRF shapes; this produces a shift in the
null-distribution histogram. When we have activating voxels with
HRF shapes which are not penalised by the HRF prior
constraints then the pseudo-z-statistics will not be reduced. We
therefore have extra sensitivity when we use Bayesian inference
with informative priors constraining the HRF shape.
). The HRF constraints reduce the power in
those voxels where the linear combinations of the basis functions
do not give sensible HRF shapes; this produces a shift in the
null-distribution histogram. When we have activating voxels with
HRF shapes which are not penalised by the HRF prior
constraints then the pseudo-z-statistics will not be reduced. We
therefore have extra sensitivity when we use Bayesian inference
with informative priors constraining the HRF shape.
Figure 5:
(a) Histogram of pseudo-z-statistics obtained for the two
different models with and without HRF constraints.
Figure 5(b) Log probability-log probability
plots. These show plots of (nominal/theoretical) frequentist FPR
against that obtained empirically. The HRF constraints reduce the
power in those voxels where the linear combinations of the basis
functions do not give sensible HRF shapes; this produces a shift
in the null-distribution histogram.
 |


Next: Spatial Mixture Modelling
Up: Artificial null data
Previous: Methods

