

Next: Noise precision updates
Up: Variational Bayes Updates
Previous: Autoregressive parameter updates
Here we give the update equation for the MRF precision parameter distribution
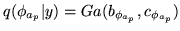 :
:
we define
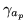 as:
as:
Even though the matrix 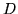 is very sparse the
computation of the
Trace
is very sparse the
computation of the
Trace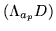 term can be very expensive to compute.
In particular, this is because
term can be very expensive to compute.
In particular, this is because
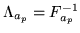 and
and 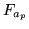 is a
is a 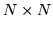 matrix whose inverse would be very
computationally expensive to compute. Therefore,
instead of computing this inverse we can compute
matrix whose inverse would be very
computationally expensive to compute. Therefore,
instead of computing this inverse we can compute 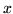 in the linear equation:
in the linear equation:
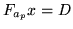 |
|
|
(46) |
Since 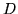 is a positive symmetric definite matrix we can take advantage of
the conjugate gradient techniques described in Golub and Van Loan (1996). At each iteration of the conjugate gradient search for
is a positive symmetric definite matrix we can take advantage of
the conjugate gradient techniques described in Golub and Van Loan (1996). At each iteration of the conjugate gradient search for 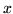 we only need to perform one
matrix multiplication of
we only need to perform one
matrix multiplication of 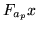 . The conjugate gradient approach
is far
quicker than solving for the inverse of
. The conjugate gradient approach
is far
quicker than solving for the inverse of 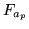 and then
multiplying by
and then
multiplying by 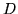 .
.
The conjugate gradient technique takes in
an initial guess of 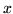 . Hence, as we iterate through the Variational Bayes
updates of our approximate posterior distributions, we can store the
the value of
. Hence, as we iterate through the Variational Bayes
updates of our approximate posterior distributions, we can store the
the value of 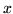 from the previous conjugate gradient solution from
the previous update of
from the previous conjugate gradient solution from
the previous update of
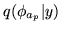 ,
and use it as the initialisation of the conjugate gradient search for
,
and use it as the initialisation of the conjugate gradient search for 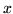 at the next update of
at the next update of
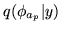 . After the first Variational
Bayes iteration this makes subsequent conjugate gradient
searches very quick to converge.
. After the first Variational
Bayes iteration this makes subsequent conjugate gradient
searches very quick to converge.


Next: Noise precision updates
Up: Variational Bayes Updates
Previous: Autoregressive parameter updates
![]() :
:
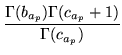
![]() . Hence, as we iterate through the Variational Bayes
updates of our approximate posterior distributions, we can store the
the value of
. Hence, as we iterate through the Variational Bayes
updates of our approximate posterior distributions, we can store the
the value of ![]() from the previous conjugate gradient solution from
the previous update of
from the previous conjugate gradient solution from
the previous update of
![]() ,
and use it as the initialisation of the conjugate gradient search for
,
and use it as the initialisation of the conjugate gradient search for ![]() at the next update of
at the next update of
![]() . After the first Variational
Bayes iteration this makes subsequent conjugate gradient
searches very quick to converge.
. After the first Variational
Bayes iteration this makes subsequent conjugate gradient
searches very quick to converge.