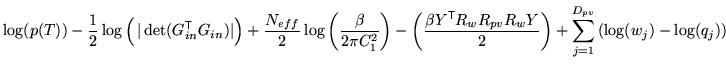Similarity Measures

Next: Test Model Up: Validation Tests Previous: Validation Tests

In order to test the usefulness of the above derivation, the posterior-based similarity function for the flat prior case is investigated. That is

$\displaystyle F_0$	$\displaystyle =$	$\displaystyle \log\left( p(T\vert Y,S,\beta) \right) + \mathrm{constant}$
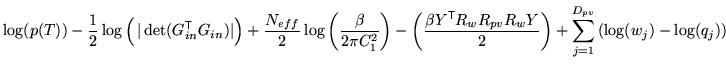	$\displaystyle =$	$\displaystyle \log(p(T)) -\frac{1}{2} \log\left( \, \vert\det(G_{in}^{\mathrm{\... ...v} R_w Y}{2} \right) + \sum_{j=1}^{D_{pv}} \left( \log(w_j) - \log(q_j) \right)$

was compared with simpler similarity functions

$\displaystyle F_1$	$\displaystyle =$	$\displaystyle Y^{\mathrm{\textsf{T}}}R_w R_{pv} R_w Y$
$\displaystyle F_2$	$\displaystyle =$	$\displaystyle \frac{1}{N_{eff}} \left( Y^{\mathrm{\textsf{T}}}R_w R_{pv} R_w Y \right)$

in the performance of some simple segmentation tasks.

In addition, the performance is compared with registration to an atlas image (generated as a separate noiseless measurement of the model).