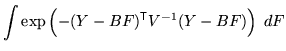 |
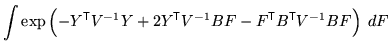 |
||
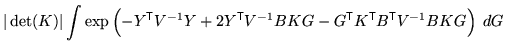 |
|||
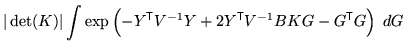 |
|||
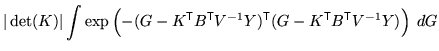 |
|||
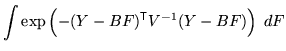 |
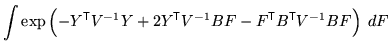 |
||
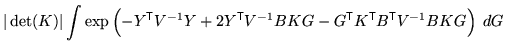 |
|||
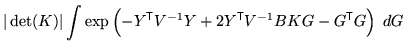 |
|||
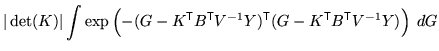 |
|||
For
![]()
![]() implies that
implies that
![]() and
and
![]() . Consequently, using the SVD decompositions
. Consequently, using the SVD decompositions
![]() and
and
![]() gives
gives
![]() .
Therefore
.
Therefore
![]() and so
and so
![]() , so that the integral is given by:
, so that the integral is given by:
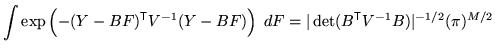 |
(17) |
For
![]() ,
,
![]() is taken to have full rank, but
is taken to have full rank, but
![]() is
not, as
is
not, as ![]() is not a square matrix, so that
is not a square matrix, so that ![]() does not
exist. Instead,
does not
exist. Instead,
![]() where
where
![]() by SVD decomposition. As
by SVD decomposition. As ![]() has dimensions
has dimensions ![]() by
by ![]() (same
as
(same
as ![]() ) then
) then
![]() is
is ![]() by
by ![]() and hence invertible (by virtue
of
and hence invertible (by virtue
of
![]() being full rank). Therefore,
being full rank). Therefore,
![]() as desired, but
as desired, but
![]() which is a projection matrix. Consequently,
which is a projection matrix. Consequently,
![]() is not zero, but is the residual projection
matix (onto the null space of
is not zero, but is the residual projection
matix (onto the null space of
![]() - the prewhitened version
of
- the prewhitened version
of ![]() ). The integral can then be written as:
). The integral can then be written as:
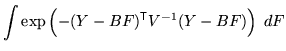 |
|||
| (18) |
For
![]() ,
,
In this case the matrix ![]() will have many linearly dependent columns
and
will have many linearly dependent columns
and
![]() cannot be achieved. Instead, let the
number of independent columns be
cannot be achieved. Instead, let the
number of independent columns be ![]() . Furthermore, let
. Furthermore, let
![]() by SVD, where
by SVD, where
![$\displaystyle D = \left[ \begin{array}{cccc} D_1 & 0 \\ 0 & 0 \end{array} \right]
$](img397.png)
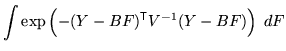 |
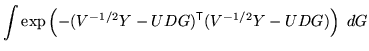 |
||
| (19) |
![$\displaystyle D_0 =\left[ \begin{array}{c} D_1 \\ 0 \end{array} \right]
$](img405.png)