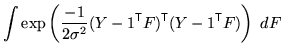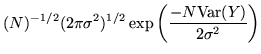

Next: Bibliography
Up: Multi-variate Gaussian Integration:
Previous: Special case: White noise
Consider 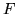 as a scalar, and
as a scalar, and
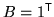 (a column vector of ones). This represents
(a column vector of ones). This represents
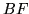 being a constant (or mean) vector. Therefore,
being a constant (or mean) vector. Therefore,
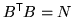 which
gives the integral as
which
gives the integral as
with
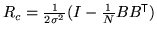 .
Note that
.
Note that
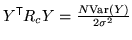 where
where
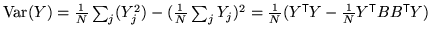 represents the estimated variance of the
data vector,
represents the estimated variance of the
data vector, 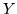 .
.