Summary

The appropriate equations to use are:

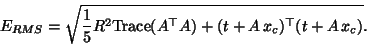$$E_{RMS} = \sqrt{\frac{1}{5} R^2 \ensuremath{\mathrm{Trace}}(A^\top A) + (t+A \, x_c)^\top (t+A \, x_c)}.$$ (35)

where

$$M = T_2 \, T_1^{-1} - I$$ (36)

$$= \left[ \begin{array}{cc} A & t \\ 0 \; 0 \; 0 & 0 \end{array} \right].$$ (37)

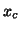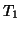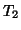$x_c$ is the centre of the volume of interest; $T_1$ and $T_2$ are the transformations (from initial to reference volume) that are being compared. Furthermore, all transformations must be world to world coordinate transformations.

Note that this implies the integration in the space of the reference volume. To use the initial volume instead, then use 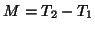$M = T_2 - T_1$, and use 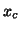$x_c$ as the world centre in the initial volume.