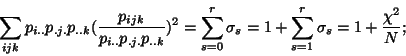

Next: FCA-modes for pharmaco-EEG
Up: -modes Correspondence Analysis
Previous: FCA-modes
As for PTA-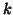 modes one will present only the case
modes one will present only the case 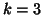 , the framework for
, the framework for 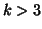 being the same.
With similar notations for a three-way table
being the same.
With similar notations for a three-way table
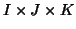 , one performs the PTA-
3modes of the quadruple:
, one performs the PTA-
3modes of the quadruple:
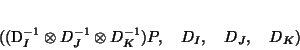 |
(26) |
This has similar properties as for FCA-2modes moreover if one notes:
for
where
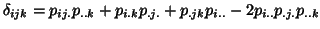 , one has the
following property:
, one has the
following property:
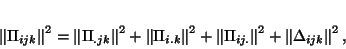 |
(27) |
where
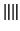 is the norm on the tensor space, i.e. using the metric
is the norm on the tensor space, i.e. using the metric
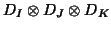 . This result dating from Lancaster(1951, 1980) was reported recently in
[1] where a particular generalisation of correspondence analysis based on
[9]'s book was derived. Equation (27) means that deviation from
three-way independence can be orthogonally decomposed into deviations from independence for the
two-way margins of the three-way table, and a three-way interaction term. Each two-way margins
deviation from independence is reminiscent of (simple) correspondence analysis. To be convinced
of this point just rewrite equation (27) as below wherein terms as in equation
(22) can be identified:
. This result dating from Lancaster(1951, 1980) was reported recently in
[1] where a particular generalisation of correspondence analysis based on
[9]'s book was derived. Equation (27) means that deviation from
three-way independence can be orthogonally decomposed into deviations from independence for the
two-way margins of the three-way table, and a three-way interaction term. Each two-way margins
deviation from independence is reminiscent of (simple) correspondence analysis. To be convinced
of this point just rewrite equation (27) as below wherein terms as in equation
(22) can be identified:
When performing the PTA-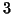 modes (26) one retrieves simply and naturally these lack of
marginal independence. The inertia or sum of squares is :
modes (26) one retrieves simply and naturally these lack of
marginal independence. The inertia or sum of squares is :
the first (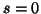 ) principal tensor being
) principal tensor being
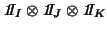 with
with 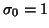 , its associated principal tensors relate to
two-way margins decompositions, i.e. each term of the second row of equation
(28). One can write a reconstruction formula similar to expressions
(23) or (24):
, its associated principal tensors relate to
two-way margins decompositions, i.e. each term of the second row of equation
(28). One can write a reconstruction formula similar to expressions
(23) or (24):
and also achieve the full decomposition (or reconstruction). Though no explicit expression of the
maximal rank 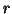 can be calculated beforehand and is a subject of research in multiway analysis.
can be calculated beforehand and is a subject of research in multiway analysis.


Next: FCA-modes for pharmaco-EEG
Up: -modes Correspondence Analysis
Previous: FCA-modes
Didier Leibovici
2001-09-04