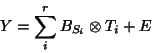

Next: Towards rank-1-ICA
Up: tr01dl1
Previous: Negentropy criterion
For a three-way data array  being a sample of size
being a sample of size  (number of voxels of the brain image) of
a random matrix
(number of voxels of the brain image) of
a random matrix 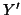 of dimensions
of dimensions 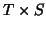 (T= number of Time points , S=number of Subjects),
different two-ways ICA can be investigated. It is possible to look for an Independent Components
in the spatial dimension associated to
(T= number of Time points , S=number of Subjects),
different two-ways ICA can be investigated. It is possible to look for an Independent Components
in the spatial dimension associated to
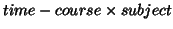 unmixing matrices. We
call it Single-ICA by analogy with single subject ICA. Note this is done with classical ICA on a
data matrix, the unmixing matrices are in fact the unmixing vectors of length the product
unmixing matrices. We
call it Single-ICA by analogy with single subject ICA. Note this is done with classical ICA on a
data matrix, the unmixing matrices are in fact the unmixing vectors of length the product 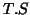 .
.
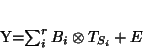 |
(9) |
Intuitively one supposes the unmixing vector as ``different" from subject to subject but the
sources should be similar i.e. we hope the sub-components (unmixing for each subjects) to be
similar. This should be considered as a random subject model but here is considered only as a
fixed subject effect as in fact we may want to look at the variation a posteriori. At this
stage in a similar way of nested PCA one could look at the SVD decomposition of the unmixing
vector as bilinear forms (
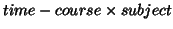 ) and probably retain the best low rank
approximation of the unmixing matrix.
) and probably retain the best low rank
approximation of the unmixing matrix.
Figure 3:
Single-ICA of the detrended time
series and subject scaled of a 12 subjects fMRI data: unmixing matrix split by subject with best
mean time-course lagged correlation to paradigm; the mean time-course is in black.
![\includegraphics[width=15cm]{rexsingleICA12_t.ps}](img46.gif) |
One gets very similar results as with PTAk for the correlation with the paradigm and
spatial representation. For the subject representation on figure (4) is slightly
different even if the interpretation of it remains the same. The variances within group seem
similar not like for PTAk where the Female group had a smaller variance.
Figure 4:
Single-ICA of the detrended time
series and subject scaled of a 12 subjects fMRI data: brain component associated to the best
correlated average time-course to paradigm; 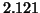 is the Jones
& Sibson approximation of the Negentropy for this component.
is the Jones
& Sibson approximation of the Negentropy for this component.
![\includegraphics[width=15cm]{rexsingleICA12_brain.ps}](img47.gif) |
Figure 5:
Single-ICA smooth SVD [4] of the unmixing matrix (fig.4) of ICA6; the
first component well correlated with the paradigm is associated with no apparent difference for
sex; on the scree plot  is for cumulated and
is for cumulated and 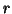 an estimation of a risk in choice dimension.
an estimation of a risk in choice dimension.
![\includegraphics[width=15cm]{rexsingleICA12_6svd.ps}](img48.gif) |
It is also possible to look for combined subject-brain Independent Components associated to
the same time-course mixing vector:
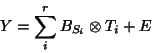 |
(10) |
It is called Multiple-ICA as the ``traditional" spatial (brain) component is multiple. One would
hope the component to reflect a ``narrow" distribution over subjects of this traditional spatial
component. This last model correspond more to the intuitive consideration that the subjects
responses to an fMRI experiment are independent identically distributed and we are looking for a
random variation of activation pattern hopefully i.e. the random variation between subjects is
accessible at each voxel. Nonetheless this last method is biased towards non-Gaussian subject
samples, i.e. as well as looking for spatial distribution the least Gaussian the method will try
to separate the subjects and with small samples of subjects this may destroy any hope of getting
similar spatial distributions.
Figure 6:
Multiple-ICA standardised mean over subjects of ICA20 and unmixing time-course.
![\includegraphics[width=15cm]{rexmultiICA12_20.ps}](img50.gif) |
Figure 7:
Multiple-ICA ICA20; the scale is different for each subject.
![\includegraphics[width=15cm]{rexmultiICA12_20b.ps}](img51.gif) |


Next: Towards rank-1-ICA
Up: tr01dl1
Previous: Negentropy criterion
Didier Leibovici
2001-09-06
![\includegraphics[width=15cm]{rexsingleICA12_t.ps}](img46.gif)
![\includegraphics[width=15cm]{rexsingleICA12_brain.ps}](img47.gif)
![\includegraphics[width=15cm]{rexsingleICA12_6svd.ps}](img48.gif)