Experiments

Various experiments have been carried out to test the performance of the HMRF-EM framework. An example is shown in the following figures. Figure 2(a) shows a simulated 3-class image sampled from an MRF model using the Gibbs sampler. The intensities for the three classes are 30, 125 and 220 respectively. Figure 2(b)-(e) show the same images with added Gaussian noise with standard deviation of 28, 47, 66, and 95. Because image contrast is what we are most interested in for examining qualities of an image, a measurement of the noise is more meaningful with image contrast being taken into account. Thus we define a measure, the noise-to-contrast ratio (NCR) as the following:

$$NCR = \frac{\text{standard deviation of the noise}}{ \text{mean inter-class contrast}}.$$

Thus, the NCRs of the four test images are 0.3, 0.5, 0.7 and 1.0, respectively. Figure 2(f)-(k) show their intensity histograms. Except for the first, each histogram exhibits severe overlap. The true parameters for the test images are listed in Table 1.

  

Figure 2: Test images for parameter estimation. (a) the original image; (b)-(e) noisy images with NCR 0.3, 0.5, 0.7, and 1.0; (f)-(k) histogram of (b)-(e).

  

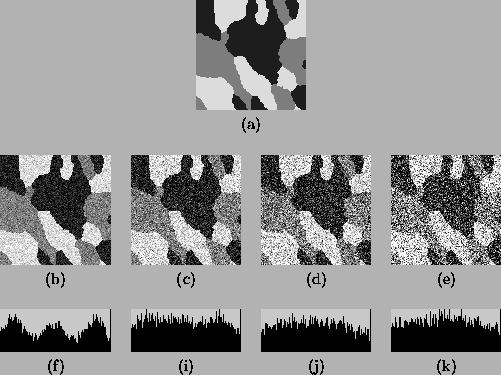Table 1: True model parameters of Figure 2(b)-(e).

  

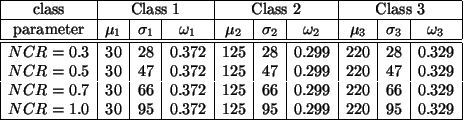Table 2: Initial parameter estimation using discriminant measure-based thresholding.

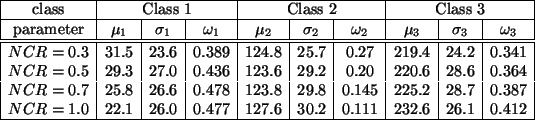The discriminant measure-based thresholding method is then applied to each of the four test images to estimate the initial parameters. Table 2 shows the results. Comparing it with Table 1, we can see that the estimates are acceptable, especially when the noise level is low. The standard FM-EM algorithm and the HMRF-EM algorithm are then applied to the four test images until there is no significant change in the value of the Q-function. To measure the segmentation accuracy, we also define the misclassification ratio (MCR), which is

$$MCR = \frac{\text{number of mis-classified pixels}}{ \text{total number of pixels}}.$$

The standard FM-EM algorithm only converges for the first image, which has the lowest noise level (NCR=0.3). In this case, the estimation results and the number of iterations K are shown in Table 3. With those estimated parameters, we reconstruct the histogram and obtain the segmentation, as shown in Figure 3. Note that, the parameter estimation is not accurate when compared with their true values listed in Table 1.

  

Table 3: Parameter estimation using the FM-EM algorithm

  

Figure 3: Parameter estimation for Figure 2(b) using the standard FM-EM algorithm. (a) the reconstructed histogram; (b) the segmentation with MCR 5.82%.

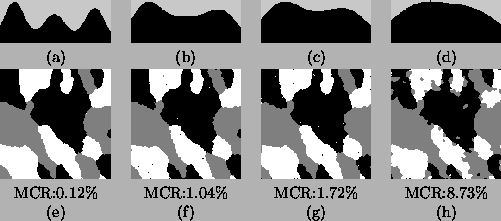
The HMRF-EM algorithm rapidly converges for all the four test images. Table 4 and Figure 4 show the results. Taking the true parameters shown in Table 1 as the references and comparing the results from the two methods, it can be seen that: (1) the HMRF-EM algorithm gives more accurate estimates for parameters; (2) the HMRF-EM algorithm provides automatic segmentation with much lower MCR.

  

Table 4: Parameter estimation using the HMRF-EM algorithm

  

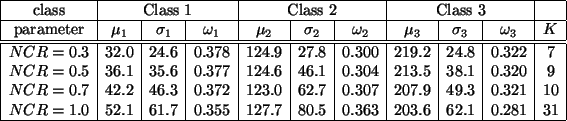Figure 4: Parameter estimation for Figure 2(b)-(e) using the HMRF-EM algorithm. top row: the reconstructed histograms; bottom row: the segmentations.