

Next: Conclusions and Perspectives
Up: tr01dl1
Previous: Single and Multiple ICA
The last point of the previous section illustrates that in fMRI we may be interested in Single-ICA
(unmixing dimension is time-subject) or in a Multiple-ICA if the multiple component is the
spatio-temporal dimension, the subject dimension being the unmixing dimension. For these two ways
of approaching ICA for multi-subject experiments a rank-one version of the ICA is certainly more
interesting. With the Single-ICA model we would look for a rank-one unmixing matrix (
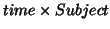 )and with the Multiple-ICA model we will look for a rank-one component (a
spatio-temporal component).
The first idea of getting a rank-one component is in nested way
of performing analysis, to do it once the ICA is finished and in summarising the unmixing matrix
by it best rank-one approximation by an SVD. Note that doing the same thing for the Multiple-ICA
approach (i.e. best approximation of the ICA component) one would not get necessary an
optimised negentropy! Note also that for the Single-ICA the two steps are optimised separately but
that usually does not mean that the rank-one unmixing is achieving maximum negentropy. This is
what we naturally did on figure 4 or when looking at the average time-course a a
pot-hoc way of describing the result.
In order to achieve a better algorithm one have to rewrite the optimisation incorporating the
rank-one ``constraint". For Single-ICA that look really like a constraint as one wants the
unmixing matrix to be of rank one. With the Multiple-ICA approach it is different as one want the
component to be of rank one. This last one is more complicated, so we will focuses on the first
one which was also the most sensible approach for fMRI data.
A simple approach for rank-one-Single-ICA is to use a penalised SVD as describe in [4] and force
``smoothing" on the principal components during optimisation as to be issued from a rebuild from
a one component ICA model. This was suggested by the equivalence (modulo some orthogonality
constraints) between penalised (smoothing as best rank-one SVD) SVD and the PTA-3modes. The
problem with this approach is that the ``smoothing" may violate too much the conditions for least
squares optimisation under smoothing constraint making the algorithm fails to converge [11].
Another rank-one-Single-ICA can be derived incorporating in the ICA algorithm a constraint on the
unmixing to be of rank-one. This is done after every updating unmixing vector then alternating
uptdating the Newton algorithm for best direction and best least squares rank-one approximation of
the unmixing vector put as a matrix
)and with the Multiple-ICA model we will look for a rank-one component (a
spatio-temporal component).
The first idea of getting a rank-one component is in nested way
of performing analysis, to do it once the ICA is finished and in summarising the unmixing matrix
by it best rank-one approximation by an SVD. Note that doing the same thing for the Multiple-ICA
approach (i.e. best approximation of the ICA component) one would not get necessary an
optimised negentropy! Note also that for the Single-ICA the two steps are optimised separately but
that usually does not mean that the rank-one unmixing is achieving maximum negentropy. This is
what we naturally did on figure 4 or when looking at the average time-course a a
pot-hoc way of describing the result.
In order to achieve a better algorithm one have to rewrite the optimisation incorporating the
rank-one ``constraint". For Single-ICA that look really like a constraint as one wants the
unmixing matrix to be of rank one. With the Multiple-ICA approach it is different as one want the
component to be of rank one. This last one is more complicated, so we will focuses on the first
one which was also the most sensible approach for fMRI data.
A simple approach for rank-one-Single-ICA is to use a penalised SVD as describe in [4] and force
``smoothing" on the principal components during optimisation as to be issued from a rebuild from
a one component ICA model. This was suggested by the equivalence (modulo some orthogonality
constraints) between penalised (smoothing as best rank-one SVD) SVD and the PTA-3modes. The
problem with this approach is that the ``smoothing" may violate too much the conditions for least
squares optimisation under smoothing constraint making the algorithm fails to converge [11].
Another rank-one-Single-ICA can be derived incorporating in the ICA algorithm a constraint on the
unmixing to be of rank-one. This is done after every updating unmixing vector then alternating
uptdating the Newton algorithm for best direction and best least squares rank-one approximation of
the unmixing vector put as a matrix
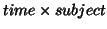 . Figure 5 shows one set
of components resulting from this approach. The problem here is that the unmixing vector length is
huge comparatively to dimension the data is susppected to lies in [2]. A dimension reduction is
usually done before ICA and the unmixing vector ``projected back" onto the original space. Because
of the rank-one contraint here one has either not to reduce the dimension before ICA making
difficult to find ICA's in a raisonnable time or to try to incorporate this reduction anyway!
. Figure 5 shows one set
of components resulting from this approach. The problem here is that the unmixing vector length is
huge comparatively to dimension the data is susppected to lies in [2]. A dimension reduction is
usually done before ICA and the unmixing vector ``projected back" onto the original space. Because
of the rank-one contraint here one has either not to reduce the dimension before ICA making
difficult to find ICA's in a raisonnable time or to try to incorporate this reduction anyway!
Figure 8:
rank one Single-ICA by constraint in an ICA: ICA28 the best correlated time-course
![\includegraphics[width=15cm]{rk1un28.ps}](img54.gif) |
This heuristic looking approach can be in fact derived directly from the rewriting of the
optimisation problem as in [10] with a tensor of rank one as argument instead of a vector.


Next: Conclusions and Perspectives
Up: tr01dl1
Previous: Single and Multiple ICA
Didier Leibovici
2001-09-06
![\includegraphics[width=15cm]{rk1un28.ps}](img54.gif)