
Next: STSAR model in FMRI
Up: Small Scale Variation
Previous: Separable Models
The simultaneous auto-regressive approach is analogous to time
series auto-regressive modelling (6):
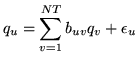 |
(5) |
where
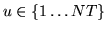 indexes a particular voxel and time
point, and
indexes a particular voxel and time
point, and
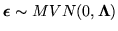 , giving:
, giving:
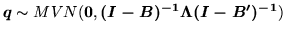 |
(6) |
where 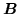 is an
is an
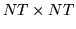 matrix whose (u,v)th
element is
matrix whose (u,v)th
element is 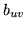 and
and
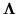 is a diagonal covariance matrix (in this paper the variances
along the diagonal of
is a diagonal covariance matrix (in this paper the variances
along the diagonal of
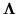 vary voxelwise but not through time).
Note that for a valid covariance matrix
vary voxelwise but not through time).
Note that for a valid covariance matrix
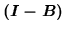 must be invertible.
In using equation 5, Wikle et al. (42) lagged the
spatial correlations by one time point. Then instead of having to
consider the entire joint distribution, we can take advantage of
conditional independence and factorise as follows:
must be invertible.
In using equation 5, Wikle et al. (42) lagged the
spatial correlations by one time point. Then instead of having to
consider the entire joint distribution, we can take advantage of
conditional independence and factorise as follows:
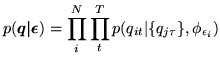 |
(7) |
where
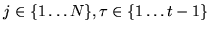 . The reason
for lagging the spatial correlations by one time point and
creating this conditional independence is to introduce directional
acyclic dependency between the
. The reason
for lagging the spatial correlations by one time point and
creating this conditional independence is to introduce directional
acyclic dependency between the 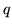 parameters. Avoiding cyclic
dependencies will improve the mixing of the MCMC sampling, whilst
introducing no loss in the usefulness of the model. This is the
approach that we will take in this work.
parameters. Avoiding cyclic
dependencies will improve the mixing of the MCMC sampling, whilst
introducing no loss in the usefulness of the model. This is the
approach that we will take in this work.


Next: STSAR model in FMRI
Up: Small Scale Variation
Previous: Separable Models