1 Introduction

Exploratory data analysis techniques like Principal Component Analysis (PCA) or Independent Component Analysis (ICA) are becoming increasingly popular for the analysis of data from functional imaging experiments, mainly for their potential to account for unknown yet structured spatio-temporal processes in neuroimaging data [McKeown et al., 1998,Strother et al., 1995,Beckmann and Smith, 2004].

Current PCA/ICA methodology typically represents the original 4-D data from a single FMRI experiment as a two-dimensional (time$\times$space) data matrix $\mbox{\protect\boldmath$X$}$, which is decomposed into a sum of $R$ outer products of individual factors:

$$\mbox{\protect\boldmath$X$}=\sum_r^R\mbox{\protect\boldmath$... ...mes \mbox{\protect\boldmath$b$}_r+\mbox{\protect\boldmath$E$}.$$

In this spatio-temporal decomposition, the entire data set is represented by different spatial processes, encoded as vectors $\mbox{\protect\boldmath$b$}_r$, and associated temporal dynamics, encoded as vectors $\mbox{\protect\boldmath$a$}_r$ and confounded by typically Gaussian noise $\mbox{\protect\boldmath$E$}$. The exact relationship within and between the sets of vectors differs according to the chosen analysis methodology, e.g. a PCA decomposition enforces orthogonality within the set of time courses and within the set of spatial maps, while an ICA decomposition relaxes the requirements on the time courses and instead places stronger restrictions (statistical independence) on the set of spatial maps. In either case, however, the underlying algorithmic concepts are rooted within the matrix algebraic framework and factorise a single 2-dimensional data matrix into time courses and spatial maps.

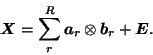
Typical neuroimaging studies, however, involve the generation of data from multiple subjects, potentially over a set of different sessions. In [Beckmann et al., 2003a] we demonstrated how these data generation scenarios fit into a hierarchical multi-level general linear modelling (GLM) framework, where - at every level - results from lower level GLM analysis are combined into a new set of higher-level estimates. While this approach would also be applicable to exploratory techniques like PCA or ICA¹, it requires resorting to model-based analysis at the higher level. In the case of exploratory data analysis techniques there is a potential loss in not modelling and infering on the entire set of data at once: when data is analysed separately there is little scope in mutually conditioning analysis results. This is less of an issue in the model-based (GLM) FMRI analysis, for it is being used to test very specific, a-priori hypotheses about the structure of the data. In the case of exploratory techniques, however, analysing multiple data all at once can improve the ability to extract spatio-temporal modes of interest and aid subsequent interpretation.

Current approaches to multi-subject group FMRI ICA decompositions involve concatenating the data either in space [Lukic et al., 2002,Svensén et al., 2002] or time [Calhoun et al., 2001], and then apply a standard two-dimensional ICA decomposition approach. This results either in time courses which are common across subjects together with subject-specific spatial maps or vice versa. Therefore, either in space or time, multiple factor estimates represent the way signal is contained in the individual subjects. In these cases the final representation at the group level differs from standard group FMRI GLM analysis, where experimenters typically are interested in finding single spatial maps which, together with single temporal modes, jointly describe an individual source process in space and time across the set of subjects². This sparse representation of signal is attractive particularly for its conceptual simplicity. Concatenating data in space or time across subjects prior to the analysis, however, effectively ignores the existence of modes of variation beyond time and space (like within-group variability) and potentially sacrifices accurate data modelling for algorithmic simplicity. Within the current group ICA methodologies, this is partly addressed by performing some heuristic meta-analysis after estimation of the individual modes, e.g. by calculating the mean temporal response or back-projection in order to obtain individual spatial maps which then can be averaged [Calhoun et al., 2001]. During the estimation stage itself, however, the multi-dimensional structure of the data is not reflected in the analysis.

In this work we are going to discuss alternative approaches based on generalising the standard bilinear (two-way) exploratory analysis methodology to higher dimensions. To this end, we are going to introduce an iterated rank-1 tensor ICA approach that will decompose a three-way data set into a set of independent spatial maps together with associated time courses and estimated subject modes. In analogy to the two-dimensional case, where ICA is often introduced as an extension to PCA, we will derive the tensor ICA technique as an extension to three-way PCA generalisations.

One such possible generalisation is known as Parallel Factor Analysis (PARAFAC³ [Harshman, 1970,Harshman and Lundy, 1994]), where a three-way array is represented by a tri-linear combination of 3 outer products:

$$\mbox{\protect\boldmath$X$}=\sum^R_r\mbox{\protect\boldmath$... ...mes \mbox{\protect\boldmath$c$}_r+\mbox{\protect\boldmath$E$}.$$

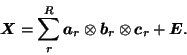
Techniques like PARAFAC have gained popularity in some scientific disciplines, e.g. in chemometrics they have been used extensively to decompose fluorescence spectroscopy data and in neuroimaging have recently been applied to EEG data to give a space-time-frequency decomposition [Miwakeichi et al., 2004]. For FMRI data, these vectors might represent variation in time, across space and between subjects⁴ and jointly form a data tensor of order 3.

In order to obtain a practical data analysis technique, the generative model needs to be augmented with a suitable cost function. Standard PARAFAC analysis generalises PCA and treats the decomposition as a sum-of-squares minimisation problem. Unlike PCA, however, the PARAFAC decomposition does not require orthogonality between any of the vectors in the representation [Harshman, 1970]. We will review the PARAFAC approach to the decomposition of three-way arrays and, using experiments on artificial FMRI data, will demonstrate that final PARAFAC estimates can exhibit significant amounts of cross-talk between estimated factors, especially in the spatial domain, with negative impact on the interpretability of results.

In the bilinear case previous research [Beckmann and Smith, 2004] has already demonstrated that the ICA approach has beneficial properties compared to a purely variance based representation as used in PCA. In particular, observed cross-talk between estimated sources was much reduced. Here, we extend this approach to a probabilistic tensor ICA model, where the generative model assumes three-way data in the presence of noise. Instead of optimising for minimum residual sum-of-squares error, we propose to optimise for maximum neg-entropy (non-Gaussianity) of estimated spatial modes.

We begin with a technical description of PARAFAC and a development of the tensor ICA method. The two techniques will then be compared on a set of artificial data sets and on a real FMRI group study.