An expansion of the basic definition 4 is sought for
small values of ![]() , which correspond to large values of
, which correspond to large values of ![]() .
This is acheived in a very similar way to the T score approximation in
the previous section.
Once again integration by parts is used to derive a
recurrence relation. Firstly, a change of variable
in equation 4 is required to get it into a more useful form.
Setting
.
This is acheived in a very similar way to the T score approximation in
the previous section.
Once again integration by parts is used to derive a
recurrence relation. Firstly, a change of variable
in equation 4 is required to get it into a more useful form.
Setting
![]() and combining equations 4 and
5 gives:
and combining equations 4 and
5 gives:
Now, consider the integral:
Combining equations 43 and 44 gives:
Combining equations 41 and 42
to gives:
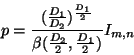 |
(47) |