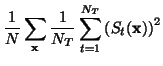 |
(50) | ||
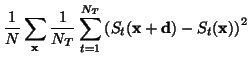 |
(51) | ||
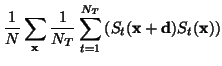 |
(52) |
To estimate the required variances simple averages are taken over the
required quantities. That is:
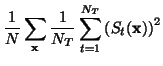 |
(50) | ||
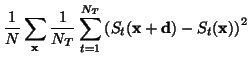 |
(51) | ||
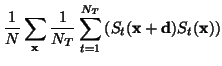 |
(52) |
The required smoothing parameters are then calculated using
equations 48 and 49. That is:
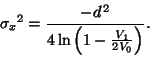 |
(53) |
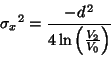 |
(54) |
Note that, because ratios are used, any constant scaling factors relating
![]() to
to
![]() will cancel.
will cancel.