
Next: Hidden Markov Random Field
Up: Hidden Markov Random Field
Previous: Finite Mixture Model
The spatial property can be modelled through different aspects,
among which, the contextual constraint is a general and
powerful one. Markov random field (MRF) theory provides a
convenient and consistent way to model context-dependent entities
such as image pixels and correlated features. This is achieved by
characterizing mutual influences among such entities using
conditional MRF distributions.
In an MRF, the sites in
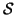 are related to one another
via a neighbourhood system, which is defined as
are related to one another
via a neighbourhood system, which is defined as
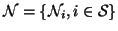 ,
where
,
where
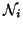 is the set of sites neighbouring i,
is the set of sites neighbouring i,
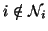 and
and
 .
A random field X said to be an MRF on
.
A random field X said to be an MRF on
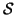 with
respect to a neighbourhood system
with
respect to a neighbourhood system
 if and only if
if and only if
Note, the neighbourhood system can be multi-dimensional. According
to the Hammersley-Clifford theorem [1], an MRF can
equivalently be characterized by a Gibbs distribution. Thus,
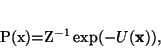 |
(5) |
where
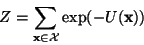 |
(6) |
is a normalizing constant called the partition function,
and
U(x) is an energy function of the form
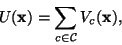 |
(7) |
which is a sum of clique potentials
Vc(x) over
all possible cliques
 .
A clique c is defined
as a subset of sites in
.
A clique c is defined
as a subset of sites in
 in which every pair of
distinct sites are neighbours, except for single-site cliques. The
value of
Vc(x) depends on the local configuration on
clique c. For more detail on MRF and Gibbs distribution see
[12].
in which every pair of
distinct sites are neighbours, except for single-site cliques. The
value of
Vc(x) depends on the local configuration on
clique c. For more detail on MRF and Gibbs distribution see
[12].


Next: Hidden Markov Random Field
Up: Hidden Markov Random Field
Previous: Finite Mixture Model
Yongyue Zhang
2000-05-11