

Next: Model Simulation and Image
Up: Hidden Markov Random Field
Previous: Markov Random Field Theory
The concept of a hidden Markov random field model is
derived from hidden Markov models (HMM), which are defined
as stochastic processes generated by a Markov chain whose state
sequence cannot be observed directly, only through a sequence of
observations. Each observation is assumed to be a stochastic
function of the state sequence. The underlying Markov chain
changes its state according to a
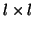 transition
probability matrix, where l is the number of states. HMMs have
been applied successfully to speech recognition
[26,30] and handwritten script recognition
[19].
Since original HMMs were designed as 1D Markov chains with first
order neighbourhood systems, it can not directly be used in 2D/3D
problems such as image segmentation. Here, we consider a special
case of a HMM, in which the underlying stochastic process is a
Markov random field (MRF), instead of a Markov chain, therefore
not restricted to 1D. We refer to this special case as a
hidden Markov random field (HMRF) model. Mathematically, an
HMRF model is characterized by the following:
Based on the above, we can write the joint probability of (X,Y)
as
transition
probability matrix, where l is the number of states. HMMs have
been applied successfully to speech recognition
[26,30] and handwritten script recognition
[19].
Since original HMMs were designed as 1D Markov chains with first
order neighbourhood systems, it can not directly be used in 2D/3D
problems such as image segmentation. Here, we consider a special
case of a HMM, in which the underlying stochastic process is a
Markov random field (MRF), instead of a Markov chain, therefore
not restricted to 1D. We refer to this special case as a
hidden Markov random field (HMRF) model. Mathematically, an
HMRF model is characterized by the following:
Based on the above, we can write the joint probability of (X,Y)
as
| P(y, x) |
= |
P(y|x)P(x) |
|
| |
= |
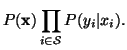 |
|
According to the local characteristics of MRFs, the joint
probability of any pair of
(Xi, Yi), given Xi's
neighbourhood configuration
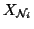 ,
is:
,
is:
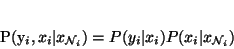 |
(9) |
Thus, we can compute the marginal probability distribution of
Yi dependent on the parameter set 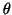 (in this case, we
treat
(in this case, we
treat 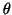 as a random variable) and
as a random variable) and
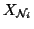 ,
,
where
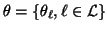 .
We call
this the hidden Markov random field (HMRF) model. Note, the
concept of an HMRF is different from that of an MRF in the sense
that the former is defined with respect to a pair of random
variable families (X,Y) while the latter is only defined with
respect to X.
More precisely, an HMRF model can be described by the following:
.
We call
this the hidden Markov random field (HMRF) model. Note, the
concept of an HMRF is different from that of an MRF in the sense
that the former is defined with respect to a pair of random
variable families (X,Y) while the latter is only defined with
respect to X.
More precisely, an HMRF model can be described by the following:
-
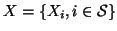 - hidden MRF, with prior distribution
p(x);
- hidden MRF, with prior distribution
p(x);
-
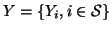 - observable random field,
with emission probability distribution
p(yi|xi) for each yi;
- observable random field,
with emission probability distribution
p(yi|xi) for each yi;
-
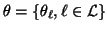 - the set
of parameters involved in the above distributions.
- the set
of parameters involved in the above distributions.
If we assume the random variables Xi are independent of each
other, which means that for
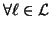 and
and
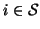 ,
we have
,
we have
then equation(10) reduces to
which is the definition of the finite mixture model. Therefore a
FM model is a degenerate special case of an HMRF model.
It is obvious from the above that the fundamental difference
between the FM model and the HMRF model lies in their different
spatial properties. The FM model is spatially independent whereas
the HMRF model may be spatially dependent. Therefore, the HMRF
model is more flexible for image modelling in the sense that it
has the ability to encode both the statistical and spatial
properties of an image.
With a Gaussian emission distribution, the FM model is usually
known as the finite Gaussian Mixture (FGM) or finite
normal mixture (FNM) model. More specifically, the observable
random variables have the following density function:
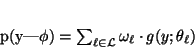 |
(11) |
where
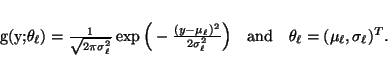 |
(12) |
Similarly, an HMRF model with a Gaussian emission distribution can
be specified as:
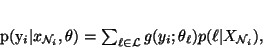 |
(13) |
where g and
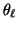 are defined as in (12). We refer
to this type of HMRF as the Gaussian hidden Markov random
field (GHMRF) model.
are defined as in (12). We refer
to this type of HMRF as the Gaussian hidden Markov random
field (GHMRF) model.


Next: Model Simulation and Image
Up: Hidden Markov Random Field
Previous: Markov Random Field Theory
Yongyue Zhang
2000-05-11