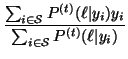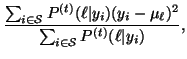

Next: Segmentation Using the HMRF-EM
Up: Segmentation of Brain MR
Previous: MRF-MAP Estimation
Model Fitting Using the EM Algorithm
A statistical model is complete only if both its functional form
and its parameters are determined. The procedure for estimating
the unknown parameters is known as model fitting. For an
HMRF model, the parameter set
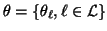 is what should be estimated. If the Gaussian
emission function is assumed for the observable random variable
y, the mean and standard deviation of each Gaussian class are
the parameters, so that
is what should be estimated. If the Gaussian
emission function is assumed for the observable random variable
y, the mean and standard deviation of each Gaussian class are
the parameters, so that
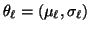 .
Since both the class label and the parameters are unknown and they
are strongly inter-dependent, the data set is said to be
``incomplete'' and the problem of parameter estimation is regarded
as an ``incomplete-data'' problem. Many techniques have been
proposed to solve this problem, among which the
expectation-maximization (EM) algorithm [11]
is the one most widely used.
The strategy underlying the EM algorithm consists of the
following: estimate the missing part as
.
Since both the class label and the parameters are unknown and they
are strongly inter-dependent, the data set is said to be
``incomplete'' and the problem of parameter estimation is regarded
as an ``incomplete-data'' problem. Many techniques have been
proposed to solve this problem, among which the
expectation-maximization (EM) algorithm [11]
is the one most widely used.
The strategy underlying the EM algorithm consists of the
following: estimate the missing part as
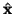 given
the current
given
the current 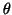 estimate and then use it to form the complete
data set
estimate and then use it to form the complete
data set
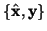 ;
new
;
new 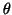 can be
estimated by maximizing the expectation of the complete-data log
likelihood,
can be
estimated by maximizing the expectation of the complete-data log
likelihood,
![${\mathcal E} \Big[\log P(\mathbf x, \mathbf
y\vert\theta)\Big]$](img85.gif) .
Mathematically, the EM algorithm can be described
by:
.
Mathematically, the EM algorithm can be described
by:
- Start
- An initial estimate
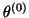 .
.
- The E-step
- Calculate the conditional expectation
- The M-step
- maximize
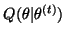 to obtain
the next estimate
to obtain
the next estimate
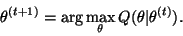 |
(23) |
Let
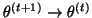 and repeat from
the E-step.
and repeat from
the E-step.
Under certain reasonable conditions, EM estimates converge locally
to the ML estimates [32].
For the GHMRF field model, the intensity distribution function,
dependent on the parameter set 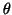 ,
is
,
is
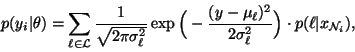 |
(24) |
where
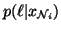 is the locally dependent
probability of
is the locally dependent
probability of 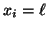 and the parameter set
and the parameter set
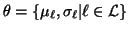 .
The Q-function is then formulated as
.
The Q-function is then formulated as
![\begin{displaymath}Q = \sum_{i \in \mathcal S}\sum_{\ell \in {\mathcal
L}}\lef...
...ell-\frac{(y_i-\mu_\ell)^2}{2\sigma_\ell^2}\right]+C\right\},
\end{displaymath}](img96.gif) |
(25) |
where
 .
Applying the EM algorithm, we obtain
.
Applying the EM algorithm, we obtain
which are the same update equations for the FGM model
[4], except that
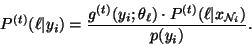 |
(28) |
The calculation of the conditional probability
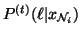 involves estimation of the
class labels, which are obtained through MRF-MAP estimation -
Equation (21). We refer to this HMRF model-based EM
algorithm as a HMRF-EM algorithm and the standard FM model-based
EM algorithm as a FM-EM algorithm.
involves estimation of the
class labels, which are obtained through MRF-MAP estimation -
Equation (21). We refer to this HMRF model-based EM
algorithm as a HMRF-EM algorithm and the standard FM model-based
EM algorithm as a FM-EM algorithm.


Next: Segmentation Using the HMRF-EM
Up: Segmentation of Brain MR
Previous: MRF-MAP Estimation
Yongyue Zhang
2000-05-11
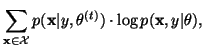
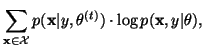
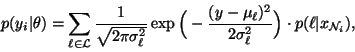
![\begin{displaymath}Q = \sum_{i \in \mathcal S}\sum_{\ell \in {\mathcal
L}}\lef...
...ell-\frac{(y_i-\mu_\ell)^2}{2\sigma_\ell^2}\right]+C\right\},
\end{displaymath}](img96.gif)