

Next: Paired -tests
Up: Examples
Previous: Numerical simulation
In the case of repeated measures, where some or all  subjects were scanned more than once, we might want to account for a possible difference in the between-subject variance and the between-session variance of the same subject. Thus, we simply extend the previous model to write
subjects were scanned more than once, we might want to account for a possible difference in the between-subject variance and the between-session variance of the same subject. Thus, we simply extend the previous model to write
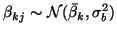
and
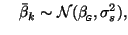
where
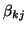 denotes the first-level parameter for subject
denotes the first-level parameter for subject 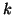 obtained at session
obtained at session 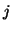 ,
,
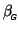 is the population mean,
is the population mean,
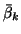 is the subject-specific mean,
is the subject-specific mean,
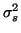 is the between-subject variance and
is the between-subject variance and
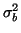 is the between-session variance. Note that this can be extended to the case of repeated measures under different conditions by introducing more variance terms. The existence of these additional variance terms will be reflected in the covariance matrix
is the between-session variance. Note that this can be extended to the case of repeated measures under different conditions by introducing more variance terms. The existence of these additional variance terms will be reflected in the covariance matrix
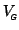 simply by allowing for off-diagonal elements. As an example, consider the case of 3 subjects each measured twice, then with
simply by allowing for off-diagonal elements. As an example, consider the case of 3 subjects each measured twice, then with
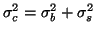 where, for simplicity, we order the subjects in pairs appropriately. Hence, we can simply adjust any covariance structure
where, for simplicity, we order the subjects in pairs appropriately. Hence, we can simply adjust any covariance structure
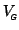 at the group level to take account of the existence of repeated measurements. Alternatively, note that because our previous results extend to multi-level GLMs, we can simply combine the different sessions per subject on a second level and calculate group parameters of interest in a third level.
at the group level to take account of the existence of repeated measurements. Alternatively, note that because our previous results extend to multi-level GLMs, we can simply combine the different sessions per subject on a second level and calculate group parameters of interest in a third level.


Next: Paired -tests
Up: Examples
Previous: Numerical simulation
Christian Beckmann
2003-07-16
![\begin{displaymath}
V_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}=\left[
...
..._{s} \\
&&&& \sigma^2_{s} & \sigma^2_{c}
\end{array}\right],
\end{displaymath}](img180.png)