Examples

In this section we show how various group level parameters of interest can easily be calculated within the GLM framework. This amounts to specifying a suitable group design matrix 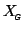$X_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}$, a covariance structure 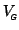$V_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}$ and possibly a contrast vector 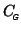$C_{_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}}$. 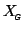Note that unlike the case of first-level designs, the mean parameter value is often of interest and hence the design matrix, $X_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}$, must always model the group mean activation, that is, the unit vector must always be included in the span of $X_{\mbox{\tiny\textit{\sffamily {$\!$G}}}}^{\mbox{}}$.

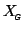For several of the examples it is easy to show the added benefit of the proposed framework using numerical simulations. These principally contrast the heteroscedastic model (allowing for different individual first-level variances) with the homoscedastic model (where first-level variances are assumed to be identical). These comparisons show substantial increases in 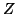$Z$-statistics over a wide range of realistic scenarios.