| (18) |
The general form of the Sherman-Morrison-Woodbury formula [8] is
Also, the inverse for a matrix in block form is given by
![$\displaystyle \left[ \begin{array}{cc} A & B \\ B^{\mbox{\scriptsize\textit{\sf...
...1}}}}B \right)^{\mbox{\scriptsize\textit{\sffamily {-1}}}}
\end{array} \right].$](img211.png) |
Theorem A:
Any model of the form
![$\displaystyle Y = \left[ X_1 \; \; Z_1 \right] \left[ \begin{array}{c} \beta_1 \\ \alpha_1 \end{array} \right] + \epsilon
$](img212.png)
![$\displaystyle Y = \left[ X_2 \; \; Z_2 \right] \left[ \begin{array}{c} \beta_2 \\ \alpha_2 \end{array} \right] + \epsilon,
$](img213.png)
That is, the signals of interest can be made orthogonal to the confounds without affecting the estimation of the parameters or the residuals.
Proof:
The proof is by construction, where we show that orthogonalising
![]() with respect to
with respect to ![]() gives the desired results. Let
gives the desired results. Let
These equations give
![]() .
Also, the combined span of
.
Also, the combined span of ![]() and
and ![]() is clearly the same
as that of
is clearly the same
as that of ![]() and
and ![]() .
.
Now consider the covariances
![$\displaystyle \textrm{Cov}\left(\left[ \!\! \begin{array}{c} \widehat{\beta_1} ...
... D \end{array} \! \right]^{\mbox{\scriptsize\textit{\sffamily {-1}}}}\!\!\!\!.
$](img225.png)
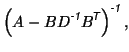 |
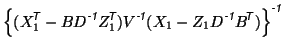 |
|||
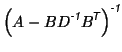 |
|||
For the first model, the parameter estimates, given by
equation 5, can be written using the matrix block inversion
formula, giving
Applying the Sherman-Morrison-Woodbury formula to the second term
in equation 12 gives
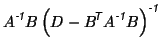 |
|||
Substituting this into equation 12 gives
|
|
Theorem B:
Given the standard GLM,
![]() , and a set of linearly
independent contrasts specified by
, and a set of linearly
independent contrasts specified by ![]() such that
such that
![]() , then an equivalent model without
contrasts, but with confounds, exists in the form
, then an equivalent model without
contrasts, but with confounds, exists in the form
![$\displaystyle Y = \left[ X_2 \; \; Z_2 \right] \left[ \begin{array}{c} b \\ \alpha \end{array}\right] + \epsilon.
$](img245.png)
Proof:
The proof is, again, by construction. Firstly, let ![]() be a set of
contrasts that when combined with
be a set of
contrasts that when combined with ![]() form a complete linearly
independent set of contrasts. That is, the matrix
form a complete linearly
independent set of contrasts. That is, the matrix
![]() will be full rank (and hence invertible). Then let
will be full rank (and hence invertible). Then let
From these definitions it is easy to see that
![]() , which
represents an orthogonality condition. As before, it is straightforward to verify that the combined span of
, which
represents an orthogonality condition. As before, it is straightforward to verify that the combined span of ![]() and
and ![]() is equal to the span of
is equal to the span of ![]() . Consequently,
. Consequently,
The estimation equations for the model become
![$\displaystyle \textrm{Cov}\left(\left[ \begin{array}{c} \widehat{b} \\ \widehat{\alpha} \end{array} \right]\right)$](img256.png) |
![$\displaystyle \left[ \begin{array}{cc} (X_2^{\mbox{\scriptsize\textit{\sffamily...
...mily {-1}}}}Z_2)^{\mbox{\scriptsize\textit{\sffamily {-1}}}}\end{array}\right],$](img257.png) |
||
![$\displaystyle \left[ \begin{array}{c} (X_2^{\mbox{\scriptsize\textit{\sffamily ...
...y {$\!$T}}}}V^{\mbox{\scriptsize\textit{\sffamily {-1}}}}\end{array} \right] Y.$](img259.png) |
Thus
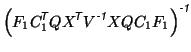 |
|||
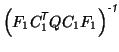 |
|||
|
|