The approach taken here to solve this problem starts by dividing the
whole (n-dimensional) volume into ![]() regions, each of which
contains no phase wrappings. Each region is then treated as a single
entity by the algorithm, with a single offset. As the number of
regions to be dealt with is much less than the number of voxels this
provides a considerable speed increase.
regions, each of which
contains no phase wrappings. Each region is then treated as a single
entity by the algorithm, with a single offset. As the number of
regions to be dealt with is much less than the number of voxels this
provides a considerable speed increase.
Now consider the interface, or boundary, between two regions, ![]() and
and ![]() .
.
The unwrapped phase, ![]() in region
in region ![]() will be related to the wrapped
phase,
will be related to the wrapped
phase, ![]() by:
by:
![]() where
where ![]() is an integer offset
that is the same for all voxels in region
is an integer offset
that is the same for all voxels in region ![]() .
.
A cost function suitable for unwrapping is one that penalises phase
differences along this interface. One good candidate is the sum of
squared difference in phase. That is:
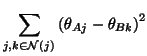 |
(2) | ||
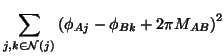 |
(3) |
The total cost over the whole volume is the sum over all the interfaces:
| (4) |
Differentiating with respect to the individual parameters, ![]() , gives
, gives
| (5) |
However, not only does this tend to generate more equations (equal to the
number of distinct interfaces) but, more importantly, only integer
values can be taken by the parameters ![]() . Therefore,
equation 6 cannot be solved exactly as it is an integer programming
problem. Finding the optimal solution (minimum cost) for such a problem is a
difficult and often time-consuming task. For example, there are
. Therefore,
equation 6 cannot be solved exactly as it is an integer programming
problem. Finding the optimal solution (minimum cost) for such a problem is a
difficult and often time-consuming task. For example, there are ![]() ``neighbouring'' solutions of the continuous solution (where
``neighbouring'' solutions of the continuous solution (where ![]() is the
number of regions).
is the
number of regions).