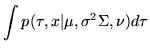

Next: Multivariate Non-central t-distribution fit
Up: Appendix
Previous: Multivariate Normal distribution
Multivariate Non-Central t distribution
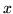 is a
is a 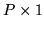 random vector and has a multivariate
non-central t distribution, denoted by
random vector and has a multivariate
non-central t distribution, denoted by
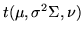 , if its density is given by:
, if its density is given by:
![$\displaystyle \mathcal{T}(x;\mu,\sigma^2 \Sigma,\nu)= \frac{\Gamma[(\nu+P)/2]}{...
...} \left(1+\frac{(x-\mu)^T\Sigma^{-1}(x-\mu)}{\sigma^2 \nu} \right)^{-(\nu+P)/2}$](img185.png) |
(24) |
where 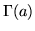 is the single-parameter Gamma function. The
non-central t distribution has
mean
is the single-parameter Gamma function. The
non-central t distribution has
mean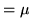 and
covariance
and
covariance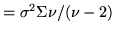 for
for 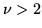 .
.
We can represent a multivariate
non-central t distribution using a two-parameter gamma distribution and
a multivariate Normal distribution in a Bayesian framework.
If we introduce
a variable 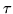 , and specify a joint posterior over
, and specify a joint posterior over
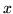 and
and 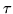 as:
as:
then the
marginal posterior for 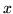 is a multivariate non-central t distribution, i.e.:
is a multivariate non-central t distribution, i.e.:


Next: Multivariate Non-central t-distribution fit
Up: Appendix
Previous: Multivariate Normal distribution
![]() is a
is a ![]() random vector and has a multivariate
non-central t distribution, denoted by
random vector and has a multivariate
non-central t distribution, denoted by
![]() , if its density is given by:
, if its density is given by:
![]() , and specify a joint posterior over
, and specify a joint posterior over
![]() and
and ![]() as:
as: