

Next: Temporal
Up: Deviance Information Criterion (DIC)
Previous: Deviance Information Criterion (DIC)
Ideally, we would use the evidence as a model adequacy measure.
The evidence is the probability of getting the data given the
model. However, obtaining the evidence is not analytic, and it is
not easy to get an accurate estimation of the evidence using MCMC
sampling. Instead of using evidence we use the Deviance
Information Criterion (DIC), which tackles
the issues of goodness of fit and model complexity using an
approximate decision-theoretic justification
(see (41)). Indeed, the DIC can be shown to be
equivalent to the evidence when the deviance is Gaussian. The
deviance is defined as the posterior distribution of the log
likelihood:
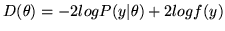 |
(23) |
where 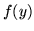 is a standardising term that does not affect model
comparison -- hence we shall deal with the first term only. The
goodness of fit of the model is then summarised by the posterior
expectation of the deviance:
is a standardising term that does not affect model
comparison -- hence we shall deal with the first term only. The
goodness of fit of the model is then summarised by the posterior
expectation of the deviance:
![$\displaystyle \bar{D} = E_{\theta\vert y}[D]$](img147.png) |
(24) |
and the complexity is given by the expected deviance minus the
deviance evaluated at the posterior expectation:
where 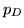 can be interpreted as the effective number of
parameters in the model. These are combined to give the overall
DIC:
can be interpreted as the effective number of
parameters in the model. These are combined to give the overall
DIC:
where the first term represents the model complexity (the
effective number of parameters) and the second term represents the
goodness of fit. The attraction of using this measure is that it
is trivial to compute when performing MCMC on the model. All that
needs to be done is to take samples of the deviance 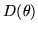 along with samples of
along with samples of 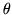 (which will be done usually anyway)
and the terms in equation 26 can be calculated to give
the DIC. Note that a good model corresponds to a low DIC. The
variations in the models we consider are:
(which will be done usually anyway)
and the terms in equation 26 can be calculated to give
the DIC. Note that a good model corresponds to a low DIC. The
variations in the models we consider are:
Subsections


Next: Temporal
Up: Deviance Information Criterion (DIC)
Previous: Deviance Information Criterion (DIC)