
Next: Likelihood
Up: Small Scale Variation
Previous: Space-Time Simultaneously specified Auto-Regressive
We assume a temporally stationary but spatially non-stationary
temporal component. It seems sensible that the spatial noise
structure would be the same through time, hence we use a
temporally stationary spatial autoregressive model. Also, the
spatial autocorrelations are assumed to be anisotropic, that is we
assume that the spatial autocorrelation is different in the three
different spatial directions.
Therefore, we use an STSAR which combines a temporally fixed
spatial AR of order 1 together with a spatially varying general
order temporal AR. It is not clear whether the spatial component
should be spatially stationary or non-stationary. Hence, we
consider both modelling approaches. In either case we have:
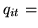 |
|
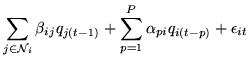 |
(8) |
where
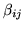 is the spatial autocorrelation between voxel
is the spatial autocorrelation between voxel
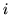 and
and 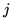 at a time lag of one,
at a time lag of one,
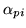 is the temporal
autocorrelation between time point
is the temporal
autocorrelation between time point 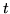 and
and 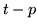 at voxel
at voxel 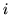 ,
and:
,
and:
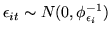 |
(9) |
The spatially stationary spatial model sets
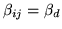 where
where 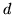 is the direction of the link
is the direction of the link 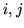 , giving:
, giving:
where
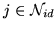 is the set of neighbouring voxels to
voxel
is the set of neighbouring voxels to
voxel 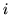 in the
in the 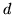 direction, there are
direction, there are 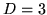 directions. The
spatially non-stationary spatial model is the same as
equation 8, but with the condition
directions. The
spatially non-stationary spatial model is the same as
equation 8, but with the condition
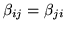 .
.


Next: Likelihood
Up: Small Scale Variation
Previous: Space-Time Simultaneously specified Auto-Regressive