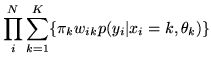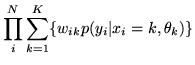

Next: Global class proportion parameters,
Up: MCMC
Previous: Control parameter,
This is sampled from using Metropolis-Hastings. With
Metropolis-Hastings, a parameter change is proposed and then
accepted or rejected according to the standard Metropolis-Hastings
rule. This requires that we recalculate the terms in the joint
posterior that change when we change
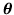 . These terms
are p(
. These terms
are p(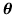 ) for all three models plus for model 1:
) for all three models plus for model 1:
| |
|
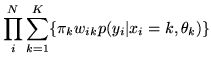 |
(29) |
or for models 2 and 3:
| |
|
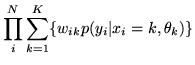 |
(30) |