

Next: Control parameter,
Up: Appendix
Previous: Gamma Distribution
MCMC
The three models we want to infer upon are described in
section 4. As described in
section 4 we infer the marginal posterior
distribution for the weights, 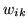 , by sampling from the full
joint posterior distribution, i.e.:
, by sampling from the full
joint posterior distribution, i.e.:
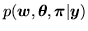 for model 1
(equation 9),
for model 1
(equation 9),
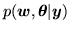 for model 2
(equation 14) or
for model 2
(equation 14) or
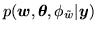 for model 3
(equation 18).
To sample these full joint posterior distributions we use Markov
Chain Monte Carlo (MCMC) techniques. See Gilks et al. (1996)
or Gamerman (1997) for an introduction to MCMC sampling. A
sample from the joint posterior distributions can be obtained by
cycling through and sampling a subset of the parameters at a time.
We now describe how we sample from each subset of parameters.
for model 3
(equation 18).
To sample these full joint posterior distributions we use Markov
Chain Monte Carlo (MCMC) techniques. See Gilks et al. (1996)
or Gamerman (1997) for an introduction to MCMC sampling. A
sample from the joint posterior distributions can be obtained by
cycling through and sampling a subset of the parameters at a time.
We now describe how we sample from each subset of parameters.
Subsections