

Next: Spatial
Up: Discrete Labels Mixture Model
Previous: Non-spatial without Class Proportions
Again, we assume spatial independence between the classification
labels as in equation 2. However, taking
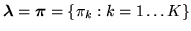 , where
, where 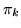 are the adaptive global class proportion parameters, the prior on
are the adaptive global class proportion parameters, the prior on
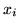 is now:
is now:
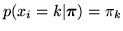 |
(4) |
The global class proportions, 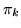 , are the relative weighting
of each of the distributions in the mixture. The prior on
, are the relative weighting
of each of the distributions in the mixture. The prior on
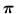 is non-informative (uniform) over the range
is non-informative (uniform) over the range
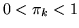 , and
, and
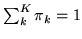 . Using this in
equation 1, the posterior becomes:
. Using this in
equation 1, the posterior becomes:
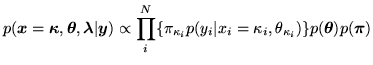 |
(5) |
![]() , where
, where ![]() are the adaptive global class proportion parameters, the prior on
are the adaptive global class proportion parameters, the prior on
![]() is now:
is now: