

Next: Basis Functions
Up: Model
Previous: Bayesian framework
Autoregressive Parameters Spatial Prior
In Penny et al. (2003) non-spatial non-informative priors were used on
the autoregressive parameters. Previous work has shown that
neighbouring voxels have similar temporal
autocorrelation (Woolrich et al., 2001; Worsley et al., 2002). Therefore, we want
to model the assumption that a priori we expect neighbouring
voxels to have similar temporal autocorrelation. To do this we use
a Gaussian conditionally specified auto-regressive (CAR) or
continuous Markov Random Field (MRF) prior (Cressie, 1993) on
each of the 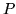 autoregressive parameter maps, i.e.
autoregressive parameter maps, i.e.
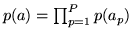 with:
with:
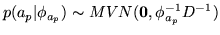 |
(7) |
where 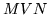 denotes a multivariate Normal distribution,
denotes a multivariate Normal distribution, 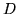 is
an
is
an
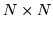 matrix whose (i,j)th element is
matrix whose (i,j)th element is 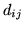 , and
, and
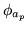 is the MRF control parameter which controls the
amount of spatial regularisation. We set
is the MRF control parameter which controls the
amount of spatial regularisation. We set 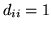 ,
,
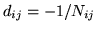 if
if 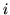 and
and 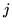 are spatial neighbours and
are spatial neighbours and
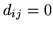 otherwise (where
otherwise (where 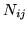 is the geometric mean of the
number of neighbours for voxels
is the geometric mean of the
number of neighbours for voxels 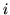 and
and 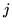 ). We also require a
hyperprior on
). We also require a
hyperprior on
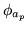 , for which we use a standard
noninformative conjugate gamma prior:
, for which we use a standard
noninformative conjugate gamma prior:
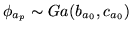 |
(8) |
Before we specify the prior for the regression parameters 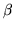 ,
we consider how we can use basis functions within this framework.
,
we consider how we can use basis functions within this framework.


Next: Basis Functions
Up: Model
Previous: Bayesian framework