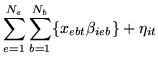

Next: Constraining Basis Function Linear
Up: Model
Previous: Autoregressive Parameters Spatial Prior
In this work we model the different HRF shapes for different
underlying conditions at different voxels using basis functions
and assuming a linear time invariant system (Josephs et al., 1997). If
we have
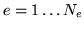 underlying conditions, and for each
condition we have
underlying conditions, and for each
condition we have
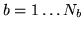 basis functions to model the HRF
for that condition for voxel
basis functions to model the HRF
for that condition for voxel 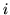 we can rewrite
equation 1 as:
we can rewrite
equation 1 as:
where
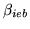 is the regression parameter for the
is the regression parameter for the 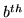 basis function of the
basis function of the 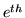 underlying condition at voxel
underlying condition at voxel 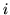 and:
and:
where 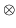 represents convolution,
represents convolution, 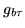 is the
is the
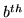 basis function and
basis function and 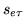 is the
is the 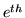 stimulus
function. Note that
stimulus
function. Note that 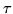 is an index at higher temporal
resolution than
is an index at higher temporal
resolution than 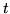 , to capture all of the HRF shape (i.e. for a
resolution of
, to capture all of the HRF shape (i.e. for a
resolution of 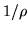 of a TR,
of a TR,
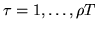 ). We obtain
). We obtain
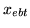 from
from
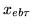 by sampling every
by sampling every 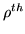
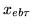 .
.


Next: Constraining Basis Function Linear
Up: Model
Previous: Autoregressive Parameters Spatial Prior